Ch11. Trees¶

约 2431 个字 28 行代码预计阅读时间 8 分钟

Basic Terminology & Properties¶

Tree: connected undirected graph with no simple circuits
Forest: undirected graph with no simple circuits (collection of trees)
一个无向图是树当且仅当在它的每对顶点之间存在唯一简单通路
选定一个根节点后，树可以被唯一地画出👆🏻（Rooted Tree）
Internal Vertex: 有孩子的点叫内点
Ordered Rooted Tree: 每个内点的孩子都排序的有根树，按从左到右的顺序
\(n\) 个顶点的树含有 \(n-1\) 条边
树都是二部图，\(K_{1,n}\) 和 \(K_{m,1}\) 是树

Unrooted Tree And Rooted Tree Counting¶

unrooted tree 类似高中化学中计数碳链个数
rooted tree 可以按最长 simple path 的长度分类计数

Counting Examples

\(n=4\)\(n=5\)\(n=6\)

unrooted

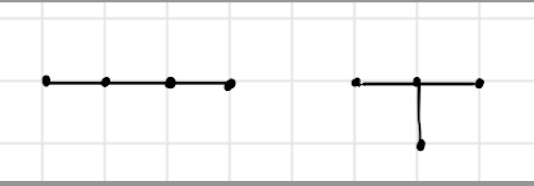
rooted

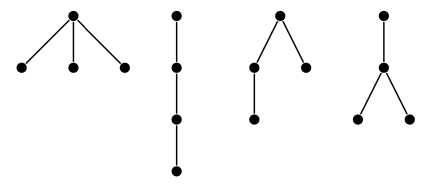
unrooted: 3
rooted: 9

unrooted: 6
rooted: 20

对于任意 \(n(n\ge 1)\)，非同构 unrooted 的计数为 OEIS 中的 A000055 序列 🔗
- 1, 1, 1, 2, 3, 6, 11, 23, 47
对于任意 \(n(n\ge 1)\)，非同构 rooted 的计数为 OEIS 中的 A000081 序列 🔗
- 1, 1, 2, 4, 9, 20, 48, 115

m-ary Tree¶

\(m\)-ary tree: 每个内点都有不超过 \(m\) 个孩子，若 \(m=2\)，称为二叉树
若每个内点都有 \(m\) 个孩子，称为 full \(m\)-ary tree (满 \(m\) 叉树)
balanced \(m\)-ary tree (平衡 \(m\) 叉树)
- 层：顶点到某点的路径长度，根节点的层为 0
- 高度：所有点层数的最大值
- 平衡：高度为 \(h\) 的 \(m\) 叉树的所有树叶都在 \(h\) 或 \(h-1\) 层，也即子树的高度差的绝对值不超过 1
A complete m-ary tree (完美 m 叉树) is a full m-ary tree in which every leaf is at the same level

Full m-ary Tree¶

\(n\) 个顶点，\(i\) 个内点，\(l\) 个叶子🍃（三个条件知一推二）

Based on: \(n=mi+1\) and \(n=l+i\)
知道 \(n\)：\(\begin{cases} i = \frac{n-1}{m} & \\ l = \frac{1+(m-1)n}{m} & \end{cases}\)
知道 \(i\)：\(\begin{cases} n=mi+1 & \\ l = (m-1)i+1 & \end{cases}\)
知道 \(l\)：\(\begin{cases} n=\frac{ml-1}{m-1} & \\ i = \frac{l-1}{m-1} & \end{cases}\)

Balanced m-ary Tree¶

高度为 \(h\)，有 \(l\) 个叶子

\(l\le m^h\)
\(h\ge \lceil \log_ml \rceil\)，若这棵树还是 full m-ary tree 取等号，即 \(h=\lceil \log_ml \rceil\)

Complete m-ary Tree¶

高度为 \(h\) 的完美 m 叉树有 \(m^h\) 个叶子🍃

Applications of Tree¶

Decision Tree (决策树)哈夫曼编码（Huffman Coding）Game Tree (博弈树)Minmax (最小化最大)

二叉搜索树每次选择左右子树就对应一次「决策」，一个子树对应着一次决策的结果
推论：基于二元比较的排序算法至少需要 \(\lceil \log n! \rceil\) 次比较，即存在下界为 \(\Omega(n\log n)\)

注意在本教材中左儿子是 0，右儿子是 1

首先，为每个字符创建一个节点，其中节点的权重为该字符出现的频率。
然后，将所有节点放入一个优先队列中，按照权重从小到大排序。
从优先队列中取出两个权重最小的节点，并将它们合并为一个新的节点，其中新节点的权重为两个子节点的权重之和。
将新节点添加回优先队列中。
重复步骤 3 和 4，直到优先队列中只剩下一个节点。这个节点就是哈夫曼树的根节点。

枚举所有可能的对局情况
Tic-tac-toe (井字棋)
...

在对抗性博弈中，一方试图最大化自己的收益，而另一方则试图最小化对手的收益

Traversal Algorithms of Trees¶

PreorderInorderPostorder

root -> left -> right

left -> root -> right

left -> right -> root

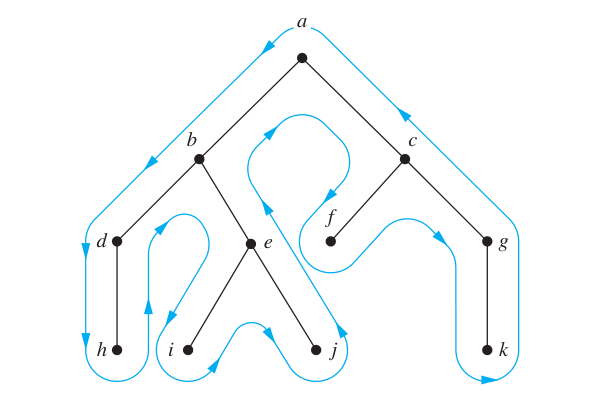
Preorder: 每当第一次访问一个顶点时就将其列出（\(a, b, d, h, e, i, j, c, f, g, k\)）
Inorder: 每当第一次访问一个叶子时就列出，第二次访问一个内点时就列出（\(h, d, b, i, e, j, a, f, c, k, g\)）
Postorder: 每当一个顶点最后一次被访问，将要返回其父亲时将其列出（\(h, d, i, j, e, b, f, k, g, c, a\)）

Prefix Form (Polish Notations)Infix FormPostfix Form (reverse Polish notation)

preorder of infix form
求值：从右到左扫描，每两个数字弹一个运算符做计算
前缀转中缀：类似后缀转中缀，从右到左 扫描

操作符的儿子是操作数

求值

1. 初始化两个栈：操作数栈和运算符栈。
2. 从左到右 扫描中缀表达式。
3. 如果遇到操作数，则将其压入操作数栈。
4. 如果遇到运算符，则比较其与运算符栈顶运算符的优先级：
      - 如果运算符栈为空，或者栈顶运算符为左括号 `(`，则直接将此运算符入栈。
      - 否则，若优先级比栈顶运算符的高，也将运算符压入运算符栈。
      - 否则，当其优先级小于等于栈顶运算符时，从操作数栈中弹出两个操作数，从运算符栈中弹出一个运算符，执行相应的计算，并将结果压入操作数栈。然后再次与运算符栈中新的栈顶运算符相比较。
5. 如果遇到括号：
      - 如果是左括号 `(`，则直接压入运算符栈。
      - 如果是右括号 `)`，则依次弹出运算符栈顶的运算符，并从操作数栈中弹出相应数量的操作数进行计算，并将结果压入操作数栈，直到遇到左括号为止。此时将这一对括号丢弃。
6. 重复步骤 2 至 5，直到表达式的最右边。
7. 将运算符栈中剩余的运算符依次弹出并执行相应的计算。
8. 最后，操作数栈中仅剩一个元素，即为中缀表达式的结果。

post order of infix form
求值：从左到右扫描，每两个数字弹一个运算符做计算

后缀转中缀

1. 从左到右 扫描后缀表达式。
2. 如果遇到操作数，则将其压入栈中。
3. 如果遇到运算符，则从栈中弹出两个操作数，将它们与运算符组合成一个带括号的子表达式，然后将子表达式压入栈中。
4. 重复步骤 2 至 4，直到后缀表达式的最右边。
5. 最终，栈中仅剩一个元素，即为中缀表达式。

Spanning Trees¶

\(G\) 是简单图，\(G\) 的生成树是包含每个顶点的子图
Theorem: 简单图连通当且仅当它有生成树

How to Find Spanning Trees?¶

Naive DFSNaive BFS

从图中选择一个起始顶点作为根节点。
使用 DFS 遍历图，记录遍历过程中访问的边。
遍历完成后，记录的边将形成图的一棵生成树。

  void dfs(int u) {
  visited[u] = 1;
  for (int v = 0; v < n; v++) {
      if (adjMatrix[u][v] && !visited[v]) {
          /* 记录边 */
          // do something
          dfs(v);
      }
  }
}

从图中选择一个起始顶点作为根节点。
使用 BFS 遍历图，记录遍历过程中访问的边。
遍历完成后，记录的边将形成图的一棵生成树。

void bfs(int s) {
    queue<int> q;
    q.push(s);
    visited[s] = 1;

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int v = 0; v < n; v++) {
            if (adjMatrix[u][v] && !visited[v]) {
                /* 记录边 */
                // do something
                q.push(v);
                visited[v] = 1;
            }
        }
    }
}

Minimum Spanning Trees¶

在有权图上找出最小生成树
普林算法（通过选点加边） & 克鲁斯卡尔算法（排序后直接选边）

How to Find Minimum Spanning Trees?¶

Prim's algorithmKruskal's algorithm

从图中任意选择一个顶点作为起始顶点。
初始化一个集合，用于存储已经访问过的顶点。将起始顶点添加到该集合中
初始化一个优先队列，用来储存访问到的边
选择一条权值最小的边并将其从队列中删除。将该边添加到最小生成树中，并将该边的未访问顶点标记为已访问，并将其添加到已访问顶点集合中。
重复步骤 4，直到所有顶点都被访问。

将图中的所有边按照权值从小到大排序。
初始化一个空集合，用于存储最小生成树的边。
按顺序遍历所有边。选择不和现在已有顶点产生回路的最小边。
重复步骤 3，直到最小生成树中包含 \(n-1\) 条边，其中 \(n\) 为图中顶点的数量。

*Spanning Trees Counting¶

* 表示此内容不在考试范围内，但可作为拓展

矩阵树定理（Matrix-Tree Theorem）是一种用于计算无向图生成树个数的定理。对于一个无向图，其生成树的个数等于其拉普拉斯矩阵的任意一个代数余子式。
- 拉普拉斯矩阵是由度数矩阵和邻接矩阵相减得到的。度数矩阵是一个对角矩阵，其对角线上的元素为各个顶点的度数。
下面是使用矩阵树定理计算无向图生成树个数的步骤：
1. 构造无向图的拉普拉斯矩阵。首先构造度数矩阵和邻接矩阵，然后将度数矩阵减去邻接矩阵。
2. 选择拉普拉斯矩阵的任意一行和一列，并将其删除，得到一个新的矩阵。
3. 计算新矩阵的行列式。
4. 新矩阵的行列式即为无向图的生成树个数。

Some Facts¶

一些常见图的生成树个数：
- \(K_n\): \(n^{n-2}\)（Cayley 公式）
- \(C_n\): \(n\)
- \(K_{m,n}\): \(mn(m-1)(n-1)\)

Supplementary Exercises¶

How many full binary trees with six vertices?

不存在这样的树。用 \(n=mi+1\) 计算发现 \(i\) 不是整数

How many vertices does a full binary tree with 50 leaves have?

\(n=2i+1,n=50+i\)，解得 \(n=99\)

If T is a full binary tree with 50 leaves, what is its minimum height?

想要最低高度，每一层需要尽量放满，即尽量平衡。\(h=\lceil \log_250 \rceil=6\)

Evaluate the arithmetic expression whose prefix representation is \(5 / * 6 2 - 5 3\)

前缀表达式求值。答案是 -1

How many spanning trees does \(C_7\) have?

答案是 7。对于一般的无向图，可以使用「矩阵树定理」来计数

The string \(2\,3\, a\,*\,x + 4 \uparrow +\,7 \uparrow\) is postfix notation for an algebraic expression. Write the expression in prefix notation.

\(\uparrow +\,2\uparrow+*\,3\,a\,x\,4\,7\)

Use Prim's algorithm to find a minimal spanning tree for this weighted graph. Use alphabetical order to break ties.

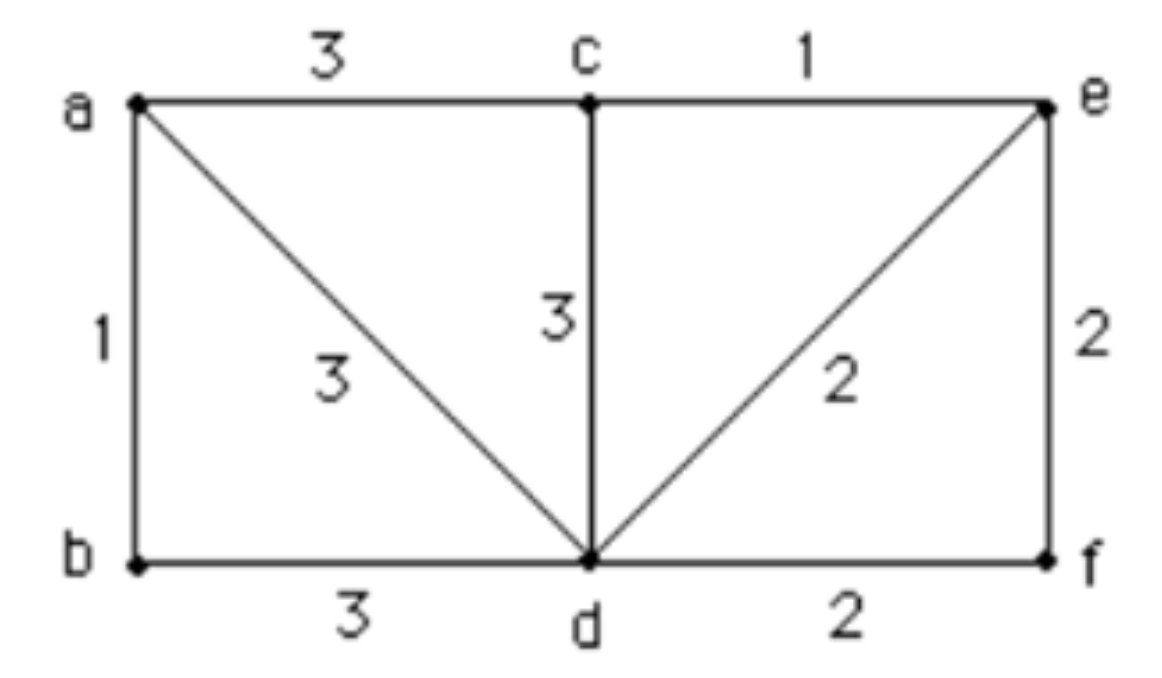
\(a-b,a-c,c-e,e-d,d-f\)，总权重为 9