Ch2. Basic Structures¶
约 1008 个字 预计阅读时间 3 分钟
Sets¶
- Subset:子集
- Proper subset:真子集
- \(\mid S \mid\) (cardinality):number of distinct elements in \(S\)
- power set
- \(A=\{a,b,c\}\),power set \(\mathcal{P}(S)\) is:
- \(\varnothing\)
- \(\{a\},\{b\},\{c\}\)
- \(\{a,b\},\{a,c\},\{b,c\}\)
- \(\{a,b,c\}\)
- \(A=\{a,b,c\}\),power set \(\mathcal{P}(S)\) is:
- \(\mathcal{P}(A) \in \mathcal{P}(B) \Rightarrow A \in B\)
- \(A\subseteq B \Rightarrow \mathcal{P}(A) \subseteq \mathcal{P}(B)\)
Set Operations¶
Union¶
- \(A \cup B\)
- \(A\subseteq A\cup B,B\subseteq A\cup B\)
- $A\subseteq C,B\subseteq C\Rightarrow A\cup B\subseteq C $
- \(|A\cup B|\leq|A|+|B|\)
- \(A\cup B=B\Leftrightarrow A\subseteq B\)
Intersection¶
- \(A\cap B\)
- \(A\cap B\subseteq A,A\cap B\subseteq B\)
- \(C\subseteq A,C\subseteq B\Rightarrow C\subseteq A\cap B\)
- \(|A\cap B|\leq|A|,|A\cap B|\leq|B|\)
- \(A\cap B=A\Leftrightarrow A\subseteq B\)
Complement¶
- \(\bar A\)
Difference¶
- \(A-B=A\cap \bar B\)
- Symmetric Differnece: \(A \oplus B=(A\cup B)-(A\cap B)\),满足结合律
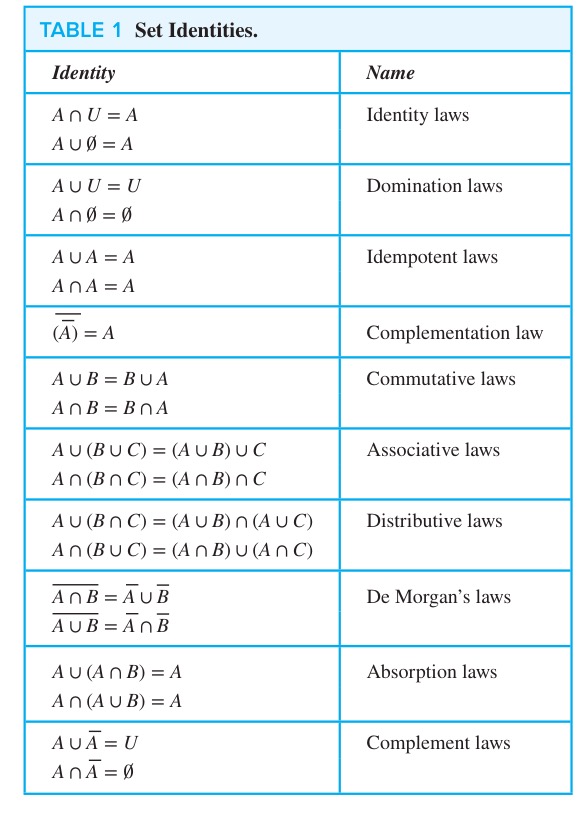
证明恒等式的方法¶
- 定义法:从集合的定义变换过去
- 证明左右两侧各是对方的子集,和👆🏻这个有点像
- 用已有的恒等式变换
- Membership Table
Cartesian Products¶
Cartesian Products of \(A_1, A_2, ..., A_n\) is \(A_1 \times A_2 \times ... \times A_n = \{(a_1,a_2,...,a_n) \mid a_i \in A_i\}\)
- Some Properties:
- \(\lvert A \rvert =m, \lvert B \rvert = n, \lvert A\times B \rvert =mn\)
- \(\lvert A\times B\rvert \neq \lvert B\times A\rvert\)
- \(\lvert A\times \varnothing\rvert = \lvert \varnothing \times A\rvert = \varnothing\)
Functions¶
Basic Functions¶
Let \(f\) be a function from \(A\) to \(B\) and \(S \subseteq A\), Denote the image of \(S\) by \(f(S)\), so that \(f(S)=\{f(s) \mid s \in S\}\).
- \(f(\varnothing) = \varnothing\)
- \(f(\{a\})=\{f(a)\}\)
- \(f(A\cup B)=f(A)\cup f(B)\)
-
\(f(A\cap B)\subseteq f(A)\cap f(B)\)
-
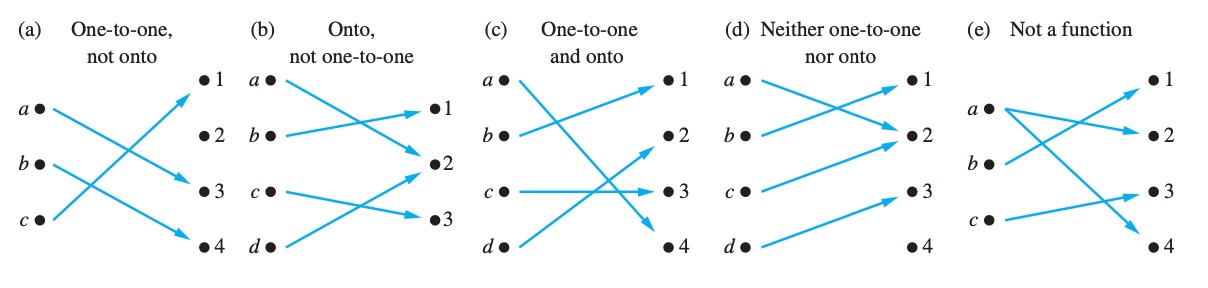
One-to-One (单射,injective)
- codomain 在 domain 里的 原像唯一
- \(\forall a\forall b(f(a)=f(b) \to a=b)\)
- Onto (满射,onto, surjective)
- codomain 在 domain 中 都有原像
- \(\forall b \in B, \exists a\in A(f(a)=b)\)
- One-to-one Correspondence (双射,bijective),一一映射,同时满足上述两种
- 计数 1-1 function:\(\lvert A \rvert=a,\lvert B \rvert=b\)
- \(a\le b\) : \(P(a, b)\) (\(P\)表示排列数)
- \(a\gt b\) : 0
-
Inverse Function (反函数)
- Let \(f\) be a bijection from \(A\) to \(B\). Denote \(f^{-1}\) as inverse function from \(B\) to \(A\).
- \(f^{-1}(y)=x \Leftrightarrow f(x)=y\)
-
Monotonic Function (单调函数)
- \(\forall x\forall y \,(x\lt y \to f(x) \lt f(y))\)
- \(\forall x\forall y \,(x\gt y \to f(x) \gt f(y))\)
Compositions of Functions¶
- Let \(g\) be a function from the set A to the set B
- Let \(f\) be a function from the set B to the set C
- The composition is denoted by \(f\circ g\), \(f\circ g(x)=f(g(x))\)
- \(g\) 的 codomain 是 \(f\) 的 domain 的子集时,\(f\circ g\) 才可被定义
- \(f,f\circ g\) 为 1-1,则 \(g\) 必须是 1-1
- \(f,f\circ g\) 为 onto,\(g\) 不一定是 onto
Floor Function & Ceiling Function¶
- Floor Function (\(\lfloor x \rfloor\))
- 不超过 \(x\) 的最大整数
- Ceiling Function (\(\lceil x \rceil\))
- 不小于 \(x\) 的最小整数

Sequences & Summations¶
- 常见求和公式
- \(\sum_{k=1}^nk=\frac{n(n+1)}{2}\)
- \(\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}{6}\)
- \(\sum_{k=1}^nk^3=\frac{n^2(n+1)^2}{4}\)
Cardinality of Sets¶
-
Definition
- \(\mid A \mid = \mid B \mid \iff\) bijection from \(A\) to \(B\)
- \(\mid A \mid \le \mid B \mid \iff\) injection from \(A\) to \(B\)
- Countablb
- finite
- same cardinality as \(\mathbb{Z}^+\)
- countable sets denoted as \(\aleph_0\)
- Uncountable: not countable
-
基本性质
- No infinite set has a smaller cardinality than a countable set.
- The union of finite number (2 or more) of countable sets is countable.
- The union of a countable number of countable sets is countable.
Cantor Diagonalization Argument¶
- 一般用于证明某个集合不可数
- 例子
(0,1) 之间的实数不可数¶
- 将 \((0,1)\) 的实数组成的集合记作 \(A\)
-
Proof:
-
\(f(n)=\frac{1}{n+1}\,(n\in \mathbb{Z}^+) \subset (0,1) \Rightarrow \mid \mathbb{Z}^+ \mid \le \mid A \mid\)
-

- This implies \(\mid \mathbb{Z}^+ \mid \neq \mid A \mid\) ↑
- So \(\mid \mathbb{Z}^+ \mid \lt \mid A \mid\)
- 这个集合的势记作 \(\aleph_1\)
-
R 和 (1,1) 有相同的势¶
- Proof:
- \(f(x)=\tan(x)\)
- \(f(x)\) is a bijection from \(-\frac{\pi}{2}, \frac{\pi}{2}\) to \((-\infty,\infty)\)
- \(\lvert \mathbb{R} \rvert = \lvert (-1,1) \rvert\)
Schroder-Bernstein Theorem¶
If A and B are sets with \(\mid A\mid \le \mid B\mid\) and \(\mid B\mid \le \mid A\mid\) then \(\mid A\mid = \mid B\mid\). In other words, if there are one-to-one functions f from A to B and g from B to A, then there is a one to one correspondence between A and B.
The cardinality of the power set of an arbitrary set has a greater cardinality than the original arbitrary set.
一些等势的结论¶
- \(\aleph_0: \mathbb{Z}, \quad \mathbb{Z}^+, \quad \mathbb{N}, \quad \mathbb{Q}, \quad \mathbb{Z}^+\times \mathbb{Z}^+, \quad \mathbb{Z}\times\mathbb{Z}\)
- \(\aleph_1: \mathbb{R}, \quad \mathbb{C}, \quad \mathcal{P}(S)\)
- \(\lvert \mathbb{R}\times\mathbb{R} \rvert = \lvert \mathbb{R} \rvert\)