Ch4. Number Theory¶
约 1272 个字 16 行代码 预计阅读时间 4 分钟
Divisibility¶
- \(n,d\) 为正整数,不超过 \(n\) 且被 \(d\) 整除的数有 \(\lfloor \frac{n}{d} \rfloor\) 个
- \(a \mid b,a\mid c \Rightarrow a\mid (b + c)\)
- \(a \mid b\Rightarrow a\mid bc,c\in \mathbb{Z}\)
- \(a\mid b,b\mid c\Rightarrow a\mid c\)
- [Division Theorem]: \(a=dq+r\, (d > 0,\, 0 \le r \lt d)\)
- \(d\) is the divisor
- \(a\) is the dividend
- \(q\) is the quotient
- \(r\) is the remainder
Modular Arithmetic¶
- Congruence Relation (同余关系):\(a\) 和 \(b\) 对 \(m\) 同余当且仅当\(m\mid a-b\),记作 \(a \equiv b \, (\bmod \,m)\),\(m\) 叫做 modulus (模数)
- 同余基本性质
- \(a=b+km\)
- \(a \equiv b \, (\bmod \,m),c \equiv d \, (\bmod \,m)\Rightarrow a + c\equiv b + d \, (\bmod \,m),ac \equiv bd \, (\bmod \,m)\)
- 同余基本性质
Arithmetic Modulo m¶
Arithmetic Modulo 是在模运算下进行的算术运算
- 定义 \(\mathbb{Z_m}\) 是小于 \(m\) 的正整数
- 定义 addition modulo \(m\): \(+_m\) => \(a+_m b=(a + b)\,(\bmod \, m)\)
- 定义 multiplication modulo \(m\): \(\cdot_m\) => \(a\cdot_m b = (a\cdot b)\,(\bmod \, m)\)
Primes¶
- prime (质数),反之 composite (合数)
- [THE FUNDAMENTAL THEOREM OF ARITHMETIC] (算术基本定理): 每个大于 1 的整数都可以唯一地表示为若干个质数的乘积,有如下形式:\(p_1^{i_1}p_2^{i_2}\cdot...\cdot p_k^{i_k}\),其中\(p1\lt p2 \lt ... \lt p_k\)
- \(n\) 为合数,整除 \(n\) 的最大质数 小于等于 \(\sqrt n\)
- 埃氏筛:用于求解不超过 \(n\) 的所有质数
- 首先,列出从 2 到 \(n\) 的所有整数
- 从 2 开始,将 2 的倍数都标记为合数
- 找到下一个未被标记为合数的整数,即 3,将 3 的倍数都标记为合数
- 重复上述步骤,直到 \(\sqrt n\) 为止
- 最后,未被标记为合数的整数即为不超过 \(n\) 的所有质数
- 质因数分解(可能看代码更直观)
private List<Integer> breakdown(int n) {
List<Integer> ans = new ArrayList<>();
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
while (n % i == 0) n /= i;
ans.add(i);
}
}
if (n != 1) {
ans.add(n);
}
return ans;
}
- Mersenne Primes (梅森数):形如 \(2^p-1\)(\(p\) 为质数)的数也为质数
- 质数的分布:不超过 \(x\) 的质数的个数(记作 \(\pi (x)\))在 \(x\to \infty\) 时趋于 \(\frac{x}{\ln x}\)
Greatest Common Divisor (GCD) & Least Common Multiple (LCM)¶
分别是最大公约数和最小公倍数
- relatively prime (互质):指两个整数的 gcd 为 1
- pairwise relatively prime: 指一系列整数两两互质
- \(ab=\gcd (a,b)\cdot \operatorname{lcm}(a,b)\)
求 GCD¶
- 暴力算法:列出两个数的质因数分解,取指数的较小者
- 欧几里得算法(辗转相除法):\(\gcd(a,b)=\gcd(b,a\bmod b)\, (a>b)\)
- 用较大的数除以较小的数,然后用余数代替较小的数
- 重复这个过程,直到余数为 0 为止
- 此时,较小的数就是两个整数的最大公约数
求 LCM¶
- 暴力算法:列出两个数的质因数分解,取指数的较大者
- 利用 \(ab=\gcd (a,b)\cdot \operatorname{lcm}(a,b)\) 求解
一些简单性质¶
- \(\gcd(a,b)=1,a\mid bc\Rightarrow a\mid c\)
- \(p\) 是质数,\(p\mid a_1a_2...a_n \Rightarrow p\mid a_i\)
- \(ac\equiv bc\,(\bmod\, m),\gcd(c,m)=1\Rightarrow a\equiv b\,(\bmod\, m)\)
裴蜀定理 🔗(Bézout's Identity)¶
- 对于任意两个整数 \(a,b\),其最大公约数为 \(\gcd(a,b)\),那么 \(ax+by=k\cdot \gcd(a,b)=m\) 有无穷多组整数解
- \(x,y\) 叫做 Bézout 系数
- 给出 \(a,b\),求解 Bézout 系数(求出 \(a,b\) 的 linear combination)可以用扩展欧几里得算法。其实在使用 GCD 的时候逆推就可以得到一组特解

Solving Linear Congruences¶
- 形如 \(ax\equiv b\,(\bmod \,m)\) 的方程
- 有解的充要条件是 \(\gcd(a,b)\mid m\)
- 为了解同余方程,我们需要引入 数论倒数。在这里,定义 \(\bar a\)为\(a\bmod m\) 的数论倒数,有 \(\bar a a\equiv 1\,(\bmod\, m)\)
- 当 \(a\) 和 \(m\) 互质且 \(m\gt 1\) 时,数论倒数存在且模 \(m\) 唯一
- 如何求解数论倒数?
- 若 \(\gcd(a,m)=1\),根据裴蜀定理,我们有 \(sa+tm=1\),两边对 \(m\) 取模,则有 \(sa\equiv 1\,(\bmod \,m)\),那么 \(s\) 即为数论倒数。由此可以看到,求解数论倒数和裴蜀定理息息相关
- 例如求 101 modulo 4620 的数论倒数(1601)
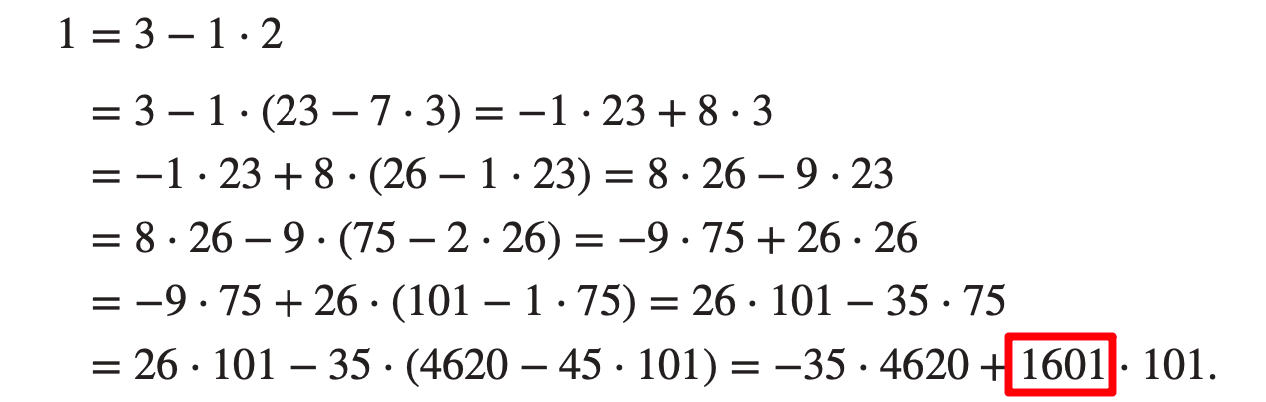
- 现在,如何求解线性同余方程?
- 我们有 \(\bar a a\equiv 1\,(\bmod\, m)\) 和 \(ax\equiv b\,(\bmod \,m)\),两边同乘 \(\bar a\) 得到 \(x\equiv b\bar a\,(\bmod \,m)\)
- 然后我们还需要验证是否 \(x\equiv b\bar a\,(\bmod \,m)\) 的每一组解都是原方程的解
The Chinese Remainder Theorem (中国剩余定理)¶
- 设 \(m_{1},...,m_{n}\) 为两两互质的正整数,\(a_{1},...,a_{n}\) 为任意正整数
- \(x\equiv a_{k}(\bmod \; m_{k}),1\le k\le n\) 称为一次同余方程组
- 记 \(m=\prod_{k=1}^{n}{m_{k}}\),对任意 \(1\le k\le n\),记 \(M_{k}=\frac{m}{m_{k}}\),\(M_{k}^{-1}\)为\(M_{k}\) 对模 \(m_{k}\) 的逆
- 同余方程组小于 \(m\) 的非负整数解唯一,为 \(x\equiv M_{1}M_{1}^{-1}a_{1}+...+M_{n}M_{n}^{-1}a_{n}\,(\bmod\;m)\)
- 例子:\(x ≡ 2 \,( \bmod \,3),\;x ≡ 3\,( \bmod \,5),\;x ≡ 2\,( \bmod \,7)\)
- \(m=3\cdot 5\cdot 7=105\)
- \(M_1=35,M_2=21,M_3=15\)
- 分别求解 \(M_1\bmod\,3\) 的逆、\(M_2\bmod\,5\) 的逆、\(M_3\bmod\,7\) 的逆
- 分别是 2、1、1
- \(x=2\cdot 35\cdot 2+1\cdot 21\cdot 3+1\cdot 15\cdot 2=233\equiv23\,(\bmod\, 105)\) (感谢 @CYH0415 纠错)
Fermat's Little Theorem¶
- \(p\) 是质数,\(p \nmid a \Rightarrow a^{p-1} \equiv 1\,(\bmod \, p)\),也即 \(a^p\equiv a\,(\bmod \, p)\)