跳转至

Ch8. Advanced Counting

约 945 个字 预计阅读时间 3 分钟

Linear Recurrence Relations

Linear, Homogeneous, Degree k, Constant Coefficients

  • Definition
    • \(a_n=c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}\)
    • \(c_k\neq 0,\, c_k\in \mathbb{R}\)
  • Solve: 解特征方程（characteristic equation），设根为 \(r_i, i\in\{1,2,...,k\}\)
    • 无重根时：\(a_n=\alpha_1r_1^n+\alpha_2r_2^n+...+\alpha_kr_k^n\)
    • 有重根时：在 \(k=2\) 时，\(a_n=\alpha_1r_0^n+\alpha_2nr_0^n\)
Proof

64zSJG

Linear, Nonhomogeneous, Degree k, Constant Coefficients

  • Definition
    • \(a_n=c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}+F(n)\)
    • \(c_k\neq 0,\, c_k\in \mathbb{R}\)
    • \(F(n)\) not zero depending only on \(n\)
  • Solve: 找特解 \(a_n^{(p)}\)，再求不含 \(F(n)\) 的递推的通解 \(a_n^{(h)}\)，则通解为 \(a_n^{(p)}+a_n^{(h)}\)
    • 特别地，当 \(F(n)\) 的形式是 \((b_tn^t+b_{t-1}n^{t-1}+...+b_1n+b_0)\cdot s^n\), \(b_i, s\in\mathbb{R}\)
      • \(s\) 不为特征根，则特解为 \((p_tn^t+p_{t-1}n^{t-1}+...+p_1n+p_0)\cdot s^n\)
      • \(s\) 为特征根且重复了 \(m\) 次，则特解为 \(n^m\cdot (p_tn^t+p_{t-1}n^{t-1}+...p_1n+p_0)\cdot s^n\)
    • 求解的时候注意特解的形式：取到哪个幂次

Generating Functions

  • Definition
    • For sequence \(a_0,a_1,a_2,...,a_k,...\)，its generating function: \(G(x)=a_0+a_1x+...+a_kx^k+...=\sum_{i=1}^\infty a_kx^k\)
    • eg: \(1+x+...+x^k=\sum_{k=0}^{\infty}x^k=\frac{1}{1-x},\, \lvert x \rvert \lt1\)
  • 求 \(G(x)\) 常用方法：
    • 对两侧积分
    • 对两侧求导
    • 构造，利用如下性质
Facts

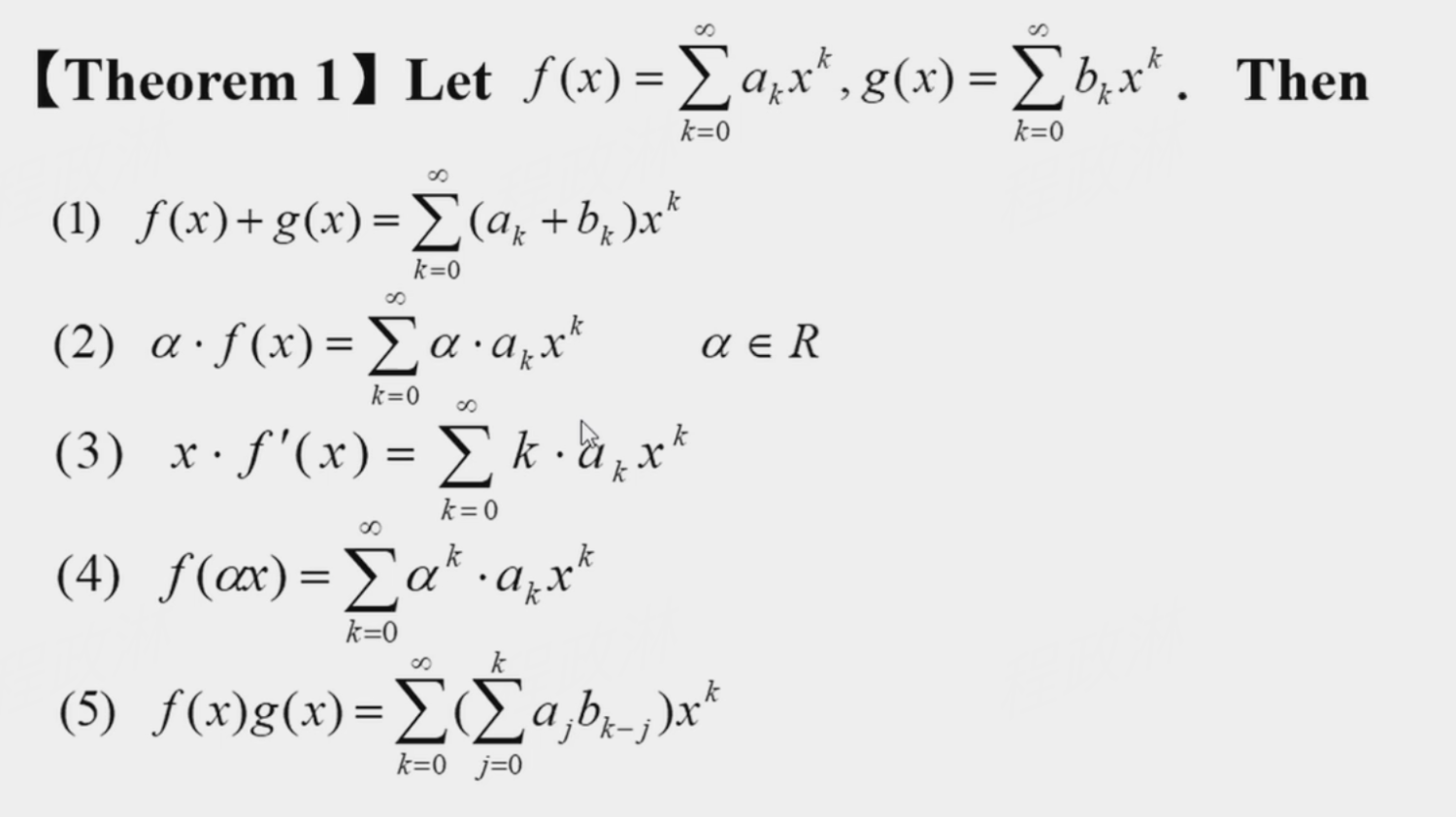
oA2jiR

Useful Facts

  • \(a_k=1\), \(G(x)=\frac{1}{1-x}\)
  • \(a_k=a^k\), \(G(x)=\frac{1}{1-ax}\)
  • \(a_k=k\), \(G(x)=\frac{x}{(1-x)^2}\)
  • \(a_k=k+1\), \(G(x)=\frac{1}{(1-x)^2}\)
  • \(a_k=C_n^k\), \(G(x)=\sum_{k=0}^\infty C_n^k\cdot x^k = (1+x)^n\)
  • \(a_k=C_n^ka^k\), \(G(x)=\sum_{k=0}^\infty C_n^ka^k\cdot x^k = (1+ax)^n\)
  • \(a_k\) 的生成函数是 \(G(x)\)，\(b_k=\sum_{i=0}^ka_i\)，则其生成函数是 \(G(x)\cdot \frac{1}{1-x}\)
Facts

87uVBr RVwXwC

Extended Binomial Coefficients

  • \(u \in \mathbb{R}\)
  • \(n\ge 0, n\in \mathbb{Z}\)
  • extended binomial coefficient is defined by \(C_u^n= \begin{cases} \frac{u(u-1)...(u-n+1)}{n!}& n \gt 0\\ 1& n=0 \end{cases}\)

  • Extended Binomial Theorem

    • \(x\in \mathbb{R}, \lvert x \rvert \lt 1, u \in \mathbb{R}\)
    • \((1+x)^u=\sum_{k=0}^{\infty}C_u^k\cdot x^k\)

  • Useful Facts: \(C_{-n}^k=(-1)^k\cdot C_{n+k-1}^k\)

Counting With Generating Functions

TODO

Solving Recurrence With Generating Functions

  • 两侧同乘 \(x^n\)
  • 从下标都有定义的初始值开始累加
  • 用生成函数 \(G(x)\) 表示 \(\sum_{0}^{\infty}a_nx^n\)
  • 用 \(G(x)\) 表示每一项，并求出 \(G(x)\)
  • 求出 \(G(x)\) 对应的系数为 \(a_n\)
一个例子

6ApD8c bh3vRR

Inculsion & Exclusion

  • \[\mid A_1\cup A_2 \cup ...\cup A_n \mid=\sum_{i=0}^n \mid A_i\mid - \sum_{1\le i \lt j \le n}\mid A_i \cap A_j \mid + \sum_{1\le i \lt j \lt k \le n}\mid A_i\cap A_j \cap A_k \mid +...+ (-1)^{n+1}\mid A_1\cap A_2 \cap ... \cap A_n \mid\]
    • 有 \(2^n-1\) 项
  • Proof: 考虑 \(a\in A_1, A_2, ... ,A_n\) 中 \(r \,(1\le r \le n)\) 个集合被计数的次数
Proof

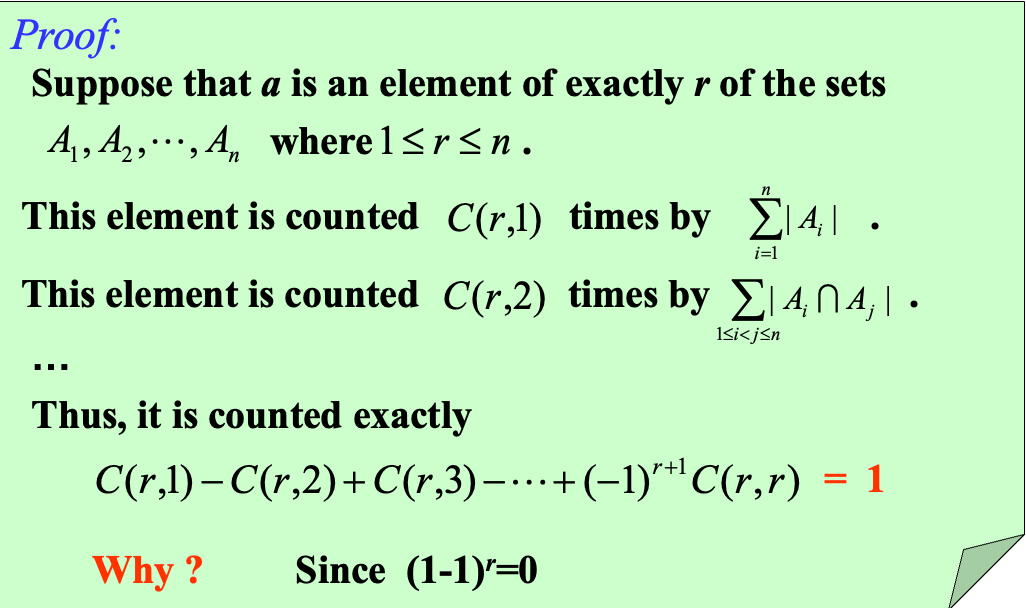
6JPkNU

  • 一般使用场景是「正难则反」
  • 即用总数减去具有某些性质的计数结果

一些例子👇🏻

  • 利用埃氏筛法，只需考虑 2, 3, 5, 7
  • 令 \(P_i\) 分别为 100 以内被 2, 3, 5, 7 整除的整数
  • 答案为总数减去所有具有 \(P_i\) 的个数
  • \(A=\{a_1,a_2,...,a_m\},\, B=\{b_1,b_2,...,b_n\}\)
  • 令 \(P_i\) 为 \(b_i\) 不在 \(A\to B\) 的 range 里
  • 答案为总数减去所有具有 \(P_i\) 的个数
  • 例如 \(C(n,1)\cdot (n-1)^m\) 表示 \(B\) 中有一个元素没有被 \(A\) 映射是 \(C(n,1)\)，剩下 \(n-1\) 个元素被 \(A\) 中的所有元素映射

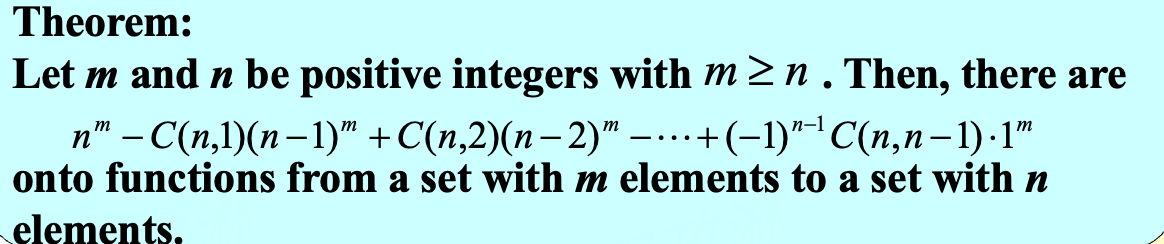
A8hHW2

  • Assign m different jobs to n different employees if every employee is assigned at least one job.
  • \(P_i: x_i \le 6\)
  • \(N(P_i)\) 表示满足 \(P_i\) 的个数
  • 答案为 \(N-(N(P_1)+N(P_2)+N(P_3)-N(P_1P_2)-N(P_1P_3)-N(P_2P_3)+N(P_1P_2P_3))\)
  • 令 \(P_i\) 为元素 \(i\) 在原来的位置上

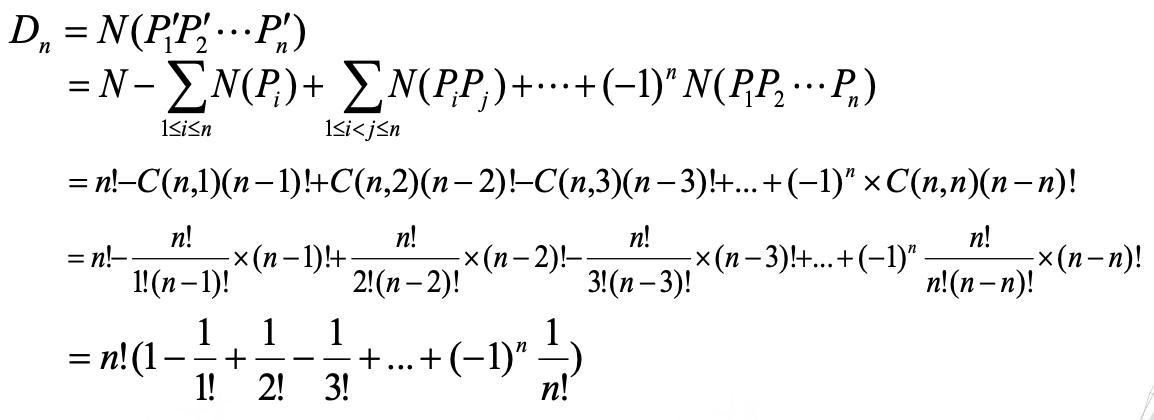
xUIywR

  • \(D_n=n!\left[1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...+(-1)^n\frac{1}{n!} \right]\)

评论