Ch10. Graphs¶
约 3656 个字 预计阅读时间 12 分钟
Basic Terminology & Properties¶
- Simple graph: 同一对顶点之间只有一条边
- Multigraph: 同一对顶点之间可能有多条边
- Pseudograph: 可能存在自环、同一对顶点之间可能有多条边
- Path: 即 \(\{v_0,v_1\},...,.\{v_{n-1},v_n\}\)，长度为 \(n\) 的路径
- 长度为 0 的路径只含一个点
- Circuit: path 首尾是同一个点
- Simple path: path 里不多次包含同一条边
- \(G(V,E)\), \(H(W,F)\)
- subgraph: 子图，\(W\subseteq V, F \subseteq E\)
- proper subgraph: 真子图，\(W\subset V, F \subset E\)
- spanning subgraph: 生成子图，\(W=V, F\subseteq E\)
- \(\deg(v)\) (度): \(\deg(v)=0\) is called isolated, \(\deg(v)=1\) is called pendant
- 自环对度的贡献为 2
- Theorem: \(G(V,E)\) with \(e\) edges, \(\sum_{v\in V}\deg(v)=2e\)
- Theorem: 无向图中度为奇数的点有偶数个
- \(\deg^-(v)\) (入度): 箭头指向的点，贡献为 1
- \(\deg^+(v)\) (出度): 箭头指出的点，贡献为 1
- Theorem: \(G(V,E)\), \(\sum_{v\in V}\deg^-(v)=\sum_{v\in V}\deg^+(v)=\lvert E \rvert\)
Special Simple Graphs¶
- denoted as \(K_n\)
- \(K_n\) has \(\frac{n(n-1)}{2}\) edges
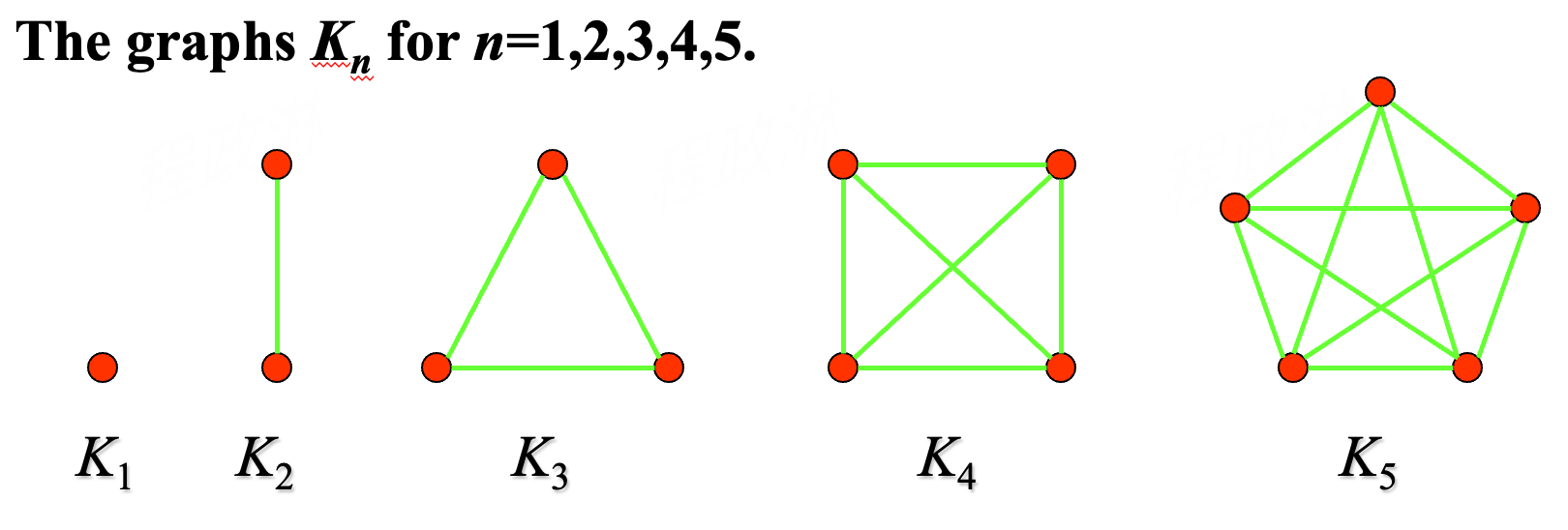
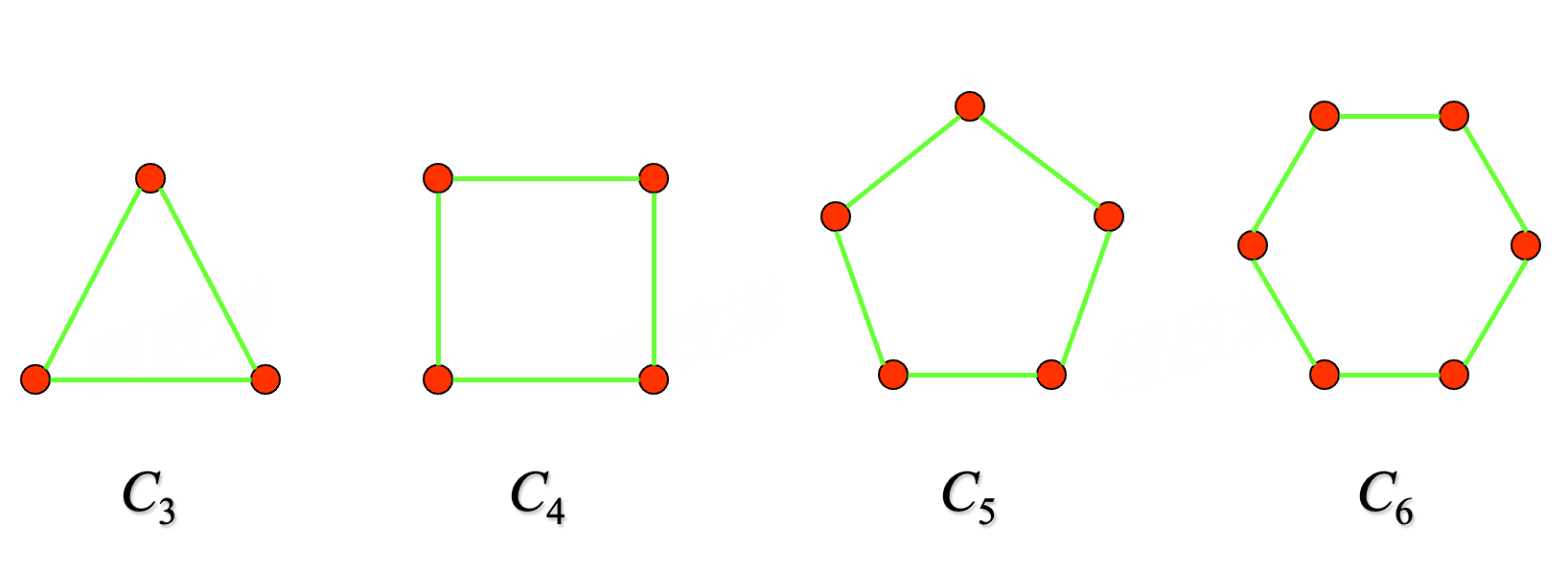
- denoted as \(C_n\)
- denoted as \(W_n(n>2)\)
- 轮图可以由环图增加一个点构造
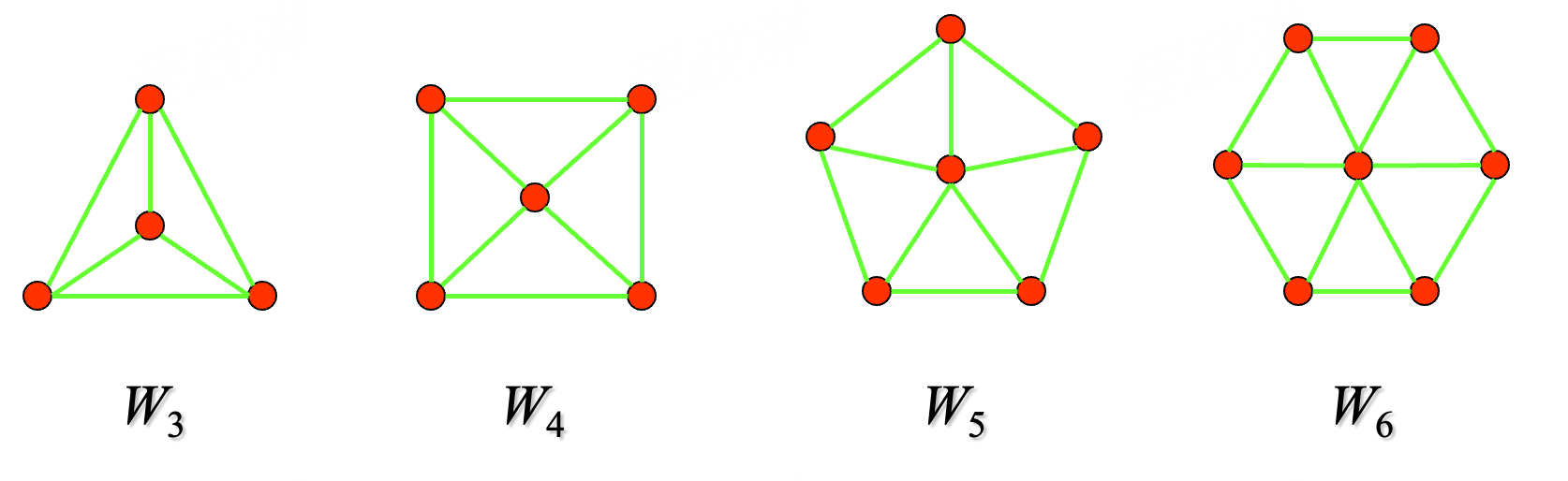
- denoted as \(Q_n\)
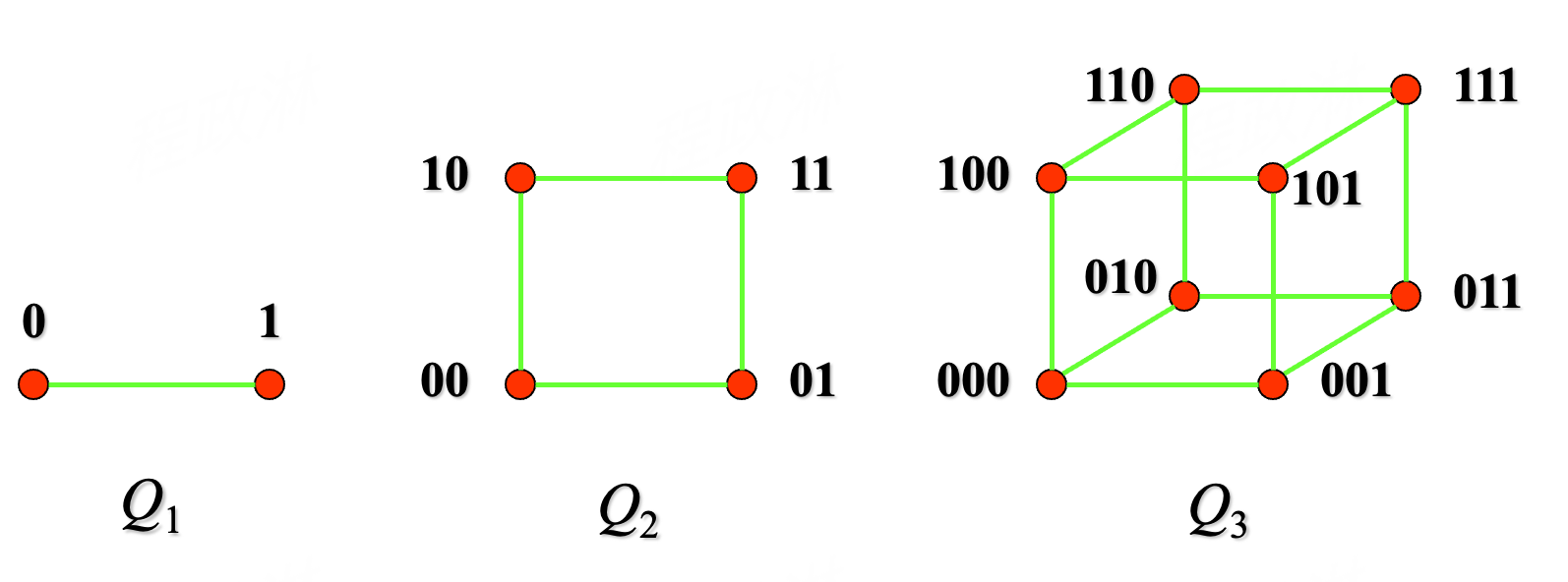
- 节点集可以分成两个 不相交 的子集，使得每条边都连接两个不同子集中的结点。即在同一个子集中的结点之间没有边相连
- Complete Bipartite Graph (完全二部图)
- 特化的二部图，两个点集分别有 \(m\) 和 \(n\) 个点，记作 \(K_{m,n}\)，一共有 \(m\cdot n\) 条边
- n-regular: 每个节点的度数都为 \(n\)
- \(K_n\) 是 n-1 regular (\(n\ge 1\))
- \(K_{n,n}\) 是 n regular
- \(C_n\) 是 n-2 regular (\(n\ge 3\))
- \(W_3\) 是 3-regular
- \(Q_n\) 是 n-regular (\(n\ge 0\))
Representing Graphs¶
- 邻接矩阵对 行 求和
- 对无向图，为 \(\deg(v)-\operatorname{loops}(v)\)
- 对有向图，为 \(\deg^+(v)\)，即出度
- 邻接矩阵对 列 求和
- 对无向图，为 \(\deg(v)-\operatorname{loops}(v)\)
- 对有向图，为 \(\deg^-(v)\)，即入度
- 记邻接矩阵为 \(A\), \(v_i\) 到 \(v_j\) 的长度为 \(r\) 的 path 的个数为：\(A^r[i][j]\)
- 对于一个有 \(n\) 个结点和 \(m\) 条边的图，它的关联矩阵是一个 \(n×m\) 的矩阵，其中行表示结点，列表示边
- 关联矩阵对 行 求和
- 对无向图，为 \(\deg(v)-\operatorname{loops}(v)\)，也即和 \(v\) 相关联的边的个数
- 对有向图，正元素之和为 \(\deg^+(v)\)，负元素之和的绝对值为 \(\deg^-(v)\)
- 关联矩阵对 列 求和
- 对无向图，无自环为 2，有自环为 1
- 对有向图，为 0，因为每条边都有一个起点和一个终点
Isomorphism of Graphs¶
- Definition: 给定两个 simple graph，存在一个「一一映射」可以从 \(G_1\) 变换到 \(G_2\)，同时保持邻接关系不发生变化
- 说明两个图同构很困难，暴力算法是 \(O(n!)\)，但我们可以较容易地说明两个图不同构
- Invariants (同构不变量): 应该在变换时保持的性质，例如节点数、边数、节点度数、path、是否可以二染色等等
Connectivity¶
- 连通：任意一对点之间都有 simple path 相连
- connected componets (连通分量)：极大连通子图
- cut vertex (割点): 从连通图里删除割点，就产生不连通的子图
- cut edge/bridge (割边，桥): 从连通图里删除割边，就产生不连通的子图
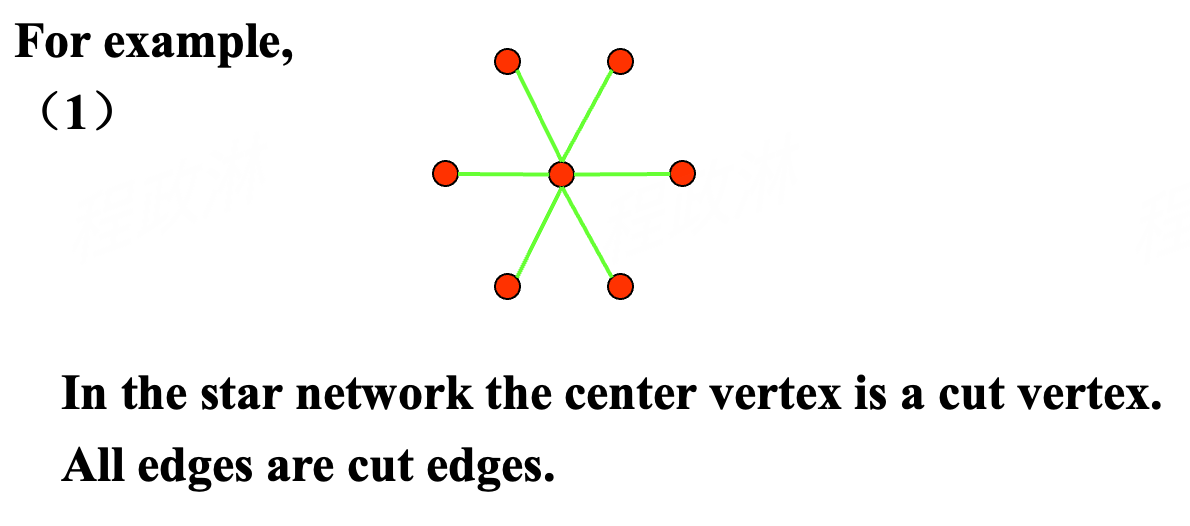
- 强连通：任意一对点 \((a,b)\)，\(a\to b\) 和 \(b\to a\) 都有 simple path
- 弱连通：将有向图看做无向图，对应无向图连通
- strongly connected componets: 极大强连通子图
- 判断一个图是否强连通？(Kosaraju 算法)
- 从同一点开始，跑两次 dfs，第一次 dfs 若遍历了全部点，则进行第二次，否则不是强连通；第二次反转所有点，再跑一次 dfs，若遍历了所有点，则强连通，否则不是
- 判断一个图是否弱连通？
- 看做无向图，跑 dfs 检查是否遍历所有点
- 如何找到强连通分量？
- 类似地，跑 Kosaraju 算法，同时记录已经访问的点，每次从还未访问的点集上跑 Kosaraju 算法
- 图的连通性也可以由邻接矩阵 \(A\) 来判定：图是连通的当且仅当 \(A+A^2+...+A^{n-1}\) 的非对角线项为正数
- 对于一个弱连通的图，若其每一个点都有 \(\deg^+(v)=\deg^-(v)\)，则该图也是强连通的
Euler Paths / Circuits¶
- Euler Path: 包含 每条边 的 simple path
- Euler Circuit: 包含每条边的 simple circuit
- Euler Graph: 包含 Euler Circuit 的图
- 每个点都是偶度数则有 欧拉回路
- 每个点都是偶度数除了两个点是奇度数，则有 欧拉路径
- 有 欧拉回路 当且仅当：
- 弱连通
- 每个点的出度、入度相等
- 有 欧拉路径 当且仅当：
- 弱连通
- 有且仅有两个点，一个入度比出度大 1，一个出度比入度大 1
How to find a path / circuit? (Fleury Algorithm)¶
- 从任意一个度数不为零的顶点开始
- 选择从该顶点出发的任意一条边，该边不能是桥（割边）
- 删除该边，并将当前顶点移动到该边的另一个端点
- 重复步骤 2 和步骤 3，直到所有边都被删除
Some Facts¶
- \(K_{n}\) 当 \(n\) 为奇数时有欧拉回路
- \(C_n\) 有欧拉回路
- \(W_n\) 没有欧拉回路
- \(Q_n\) 当 \(n\) 为偶数时有欧拉回路
- \(K_{m,n}\) 当 \(m,n\) 均为偶数时有欧拉回路
- \(K_{m,2}\)，\(m\) 为奇数有欧拉路径
- \(K_{2,n}\)，\(n\) 为奇数有欧拉路径
Applications¶
- Chinese Postman Problem
- Networking, Molecular Biology
Hamilton Paths / Circuits¶
如无特别说明，讨论哈密顿回路时皆为 无向图
- Hamilton Path: 包含 每个节点（仅一次）的 simple path
- Hamilton Circuit: 除了起点和终点包含两次，其他每个节点包含一次的 simple circuit
- Hamilton Graph: 含 Hamilton Circuit 的图
Halmiton Circuits¶
- Dirac Theorem (狄拉克定理): 如果 \(G\) 是有 \(n\) 个顶点的简单图，其中 \(n\ge3\)，并且 \(G\) 中每个顶点的 度都至少为 \(\frac{n}{2}\)，则 \(G\) 有哈密顿回路
- Ore Theorem (欧尔定理): 如果 \(G\) 是有 \(n\) 个顶点的简单图，其中 \(n\ge 3\)，并且对于 \(G\) 中每一对不 相邻的顶点 \(u\) 和 \(v\) 来说，都有 \(\deg(u)+\deg(v)\ge n\)，则 \(G\) 有哈密顿回路
- 狄拉克定理可以看做欧尔定理的推论
- 存在哈密顿图既不满足 Dirac 也不满足 Ore 的条件
- 如果一个图存在哈密顿回路，则该图是二连通的
- 二连通（biconnected）是指一个无向图中，如果从图中删除任意一个顶点，剩余的图仍然是连通的。也就是说，图中不存在割点
- 如果一个图存在哈密顿回路，则每个点的度都大于 1
- 如果一个图中存在哈密顿回路，并且该图中有一个度数为 2 的顶点，则与该顶点相连的两条边都必须属于哈密顿回路
- 在构造哈密顿回路时，如果已经经过了一个顶点，则除了用于构造哈密顿回路的两条边之外，与该顶点相连的其他边都可以不再考虑（因为哈密顿回路只能经过每个顶点恰好一次）
Hamilton Paths¶
- 如果一个图存在哈密顿路径，则该图中至多只能有两个度数为 1 的顶点
- 因为哈密顿路径的起点和终点的度数为 1，而路径上的其他顶点都至少有两条边与之相连，因此它们的度数至少为 2
Some Facts¶
- \(K_n,C_n,W_n,Q_n\) 有哈密顿回路
- \(K_{n,n}\) 有哈密顿回路
Applications¶
- Traveling Salesman Problem (TSP): 在一个带权无向图上，找出具有 最小权重 的 哈密顿回路
- 暴力算法：找出所有哈密顿回路，然后求最小，时间复杂度为 \(O(n!)\)
- 近似算法：一个著名的近似算法是 Christofides 算法，它可以保证解的质量不会超过最优解的 1.5 倍
Shortest Path Problems¶
Dijkstra Algorithm¶
- 可以求解 单源 最短路径，适用于 带权有向图 或 无向图，且图中所有边的权值都必须为 非负数
- 给定一个带权有向图或无向图 \(G=(V,E)\)，其中 \(V\) 是顶点集，\(E\) 是边集，每条边 \((u,v)\in E\) 都有一个非负的权值 \(w(u,v)\)。设 \(d[v]\) 表示从起点 \(s\) 到顶点 \(v\) 的最短距离。
- 初始化：将所有顶点的最短距离设为无穷大，即 \(d[v]=\infty\)，并将起点的最短距离设为 0，即 \(d[s]=0\)
- 创建一个集合 \(S\)，用于存储已经确定最短距离的顶点
- 对于图中的每个顶点，执行以下操作：
- 从未确定最短距离的顶点中选择一个最小的顶点 \(u\)，并将其加入集合 \(S\)
- 对于与顶点 \(u\) 相邻的每个顶点 \(v\)，如果 \(d[u]+w(u,v)<d[v]\)，则更新 \(d[v]\) 的值
- 算法结束时，\(d[v]\) 的值即为从起点 \(s\) 到顶点 \(v\) 的最短距离
Example
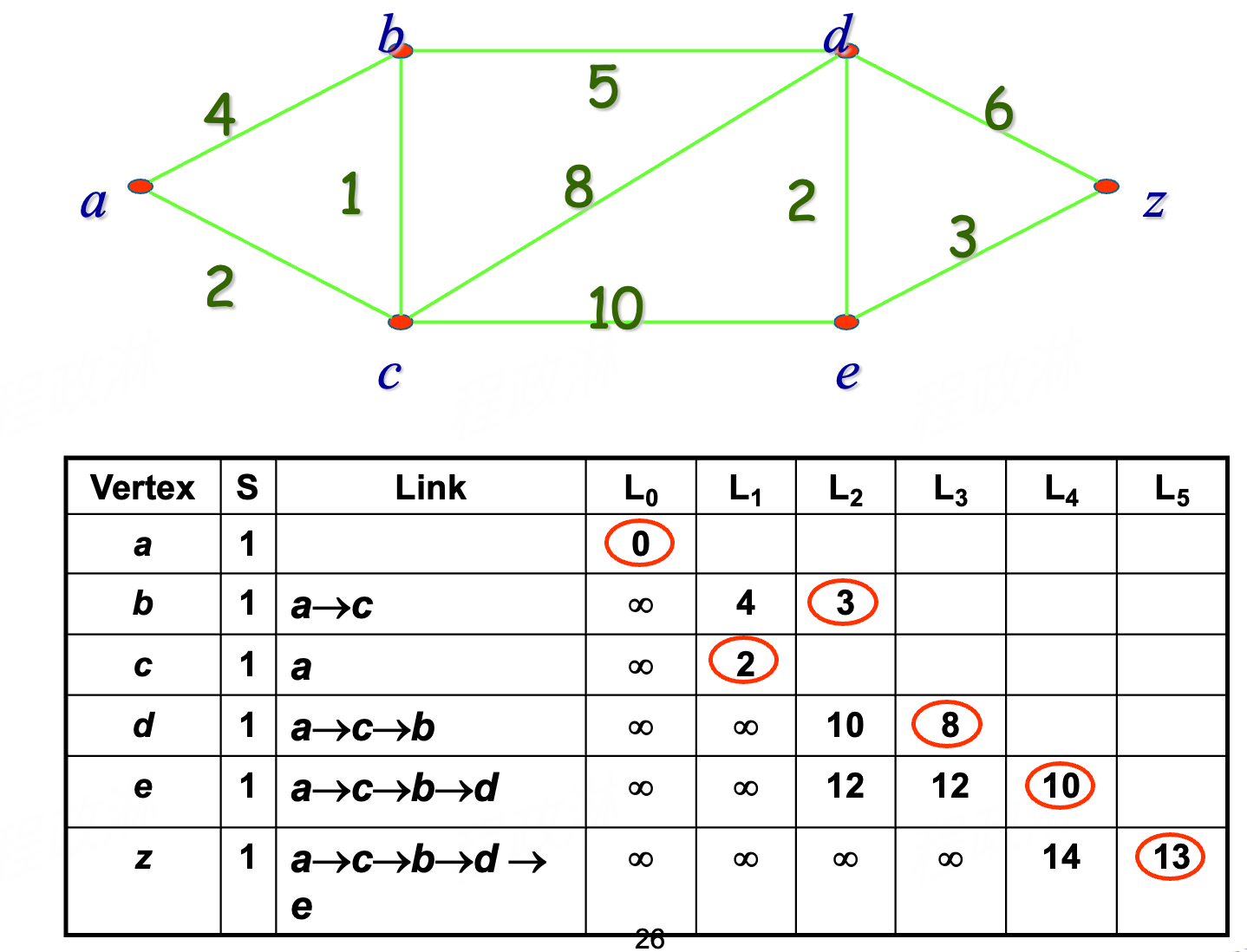
Tip
- 上述算法的时间复杂度是 \(O(V^2)\)，\(V\) 为节点个数
- 通过加入优先队列来优化后的时间复杂度为 \(O((E+V)\log V)\)
Planar Graphs¶
- Definition: 若可以在平面中画出一个图而边没有任何交叉（其中边的交叉是表示边的直线或弧线在它们的公共端点以外的地方相交），则这个图是平面图
Euler's Formula¶
- Region (面)：一个图的平面表示把平面分割成一些 Region，包括一个没有边界（boundless）的 Region
Example
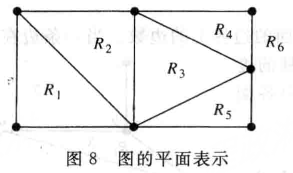
- Degree of a Region (面的度)：定义为某个面边界上的边数，若边为桥，贡献为 2
- \(\sum_{v_i\in V} \deg(v_i)=\sum_{r_i\in R} \deg(r_i)=2e\)
- \(G\) 是 connected planar simple graph，有 \(e\) 条边和 \(v\) 个顶点，\(r\) 是 \(G\) 的平面图表示中的面数，则 \(r=e-v+2\)
- 推论 1：\(G\) 是 connected planar simple graph，有 \(e\) 条边和 \(v\, (\ge 3)\) 个顶点，则 \(e\le 3v -6\)
- \(K_5\) 是非平面图
- 推论 2：\(G\) 是 connected planar simple graph，则 \(G\) 中有度不超过 5 的顶点
- 推论 3：\(G\) 是 connected planar simple graph，有 \(e\) 条边和 \(v\, (\ge 3)\) 个顶点且没有长度为 3 的环，则 \(e\le 2v-4\)
- \(K_{3,3}\) 是非平面图
- 推论 4：\(G\) 是 connected planar simple graph，有 \(e\) 条边和 \(v\, (\ge 3)\) 个顶点且每个面都有至少 \(k\) 条边（没有长度为 \(k-1\) 的环），则 \(e\le \frac{(v-2)k}{k-2}\)
- 推论 3 可以看作是推论 4 的特例
- 上面👆🏻的推论可以用来证明一个图不是平面图
- 推论 1：\(G\) 是 connected planar simple graph，有 \(e\) 条边和 \(v\, (\ge 3)\) 个顶点，则 \(e\le 3v -6\)
Kuratowski's Theorem¶
- Elementary Subdivision (初等细分)：若一个图是平面图，则通过删除一条边 \(\{u,v\}\) 并且添加一个新顶点 \(w\) 和两条边 \((u,w)\) 与 \((w,v)\) 获得的任何图也是平面图。也即，平面图中的一条边通过添加一个点的方式变成两条边，不改变其是平面图的性质
- Homeomorphic (同胚)：相同的图通过「初等细分」得到不同的图，称其之间同胚
- Theorem：一个图是 非平面图 当且仅当其包含一个同胚于 \(K_5\) 或 \(K_{3,3}\) 的子图
- 例如 Peterson 图包含 \(K_{3,3}\)，不是平面图
Graph Coloring¶
- Dual Graph (对偶图)：平面地图中，一个面对应一个点，若两个面相邻，则两个点之间有边。这样得到的图称为对偶图
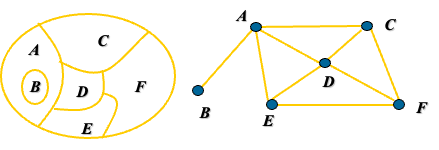
- Coloring (着色)：指对该图的每个顶点都指定一种颜色，使得没有两个相邻的顶点颜色相同
- Chromatic Number of A Graph (着色数)：着色这个图所需要的最少颜色数，记作 \(\chi(G)\)
- 一般来说，得到 \(\chi(G)=k\) 的方法是证明可以用 \(k\) 个颜色着色，而 \(k-1\) 则不能着色
- \(\chi(G)\) of \(C_n\): \(n\) 为奇数，为 3，反之为 2
- \(\chi(G)\) of \(K_n\): \(n\)
- 若简单图的着色数为 2，说明其是二分图
- 四色定理：平面图 的着色数不超过 4，非平面图可以有任意大的着色数
Applications of Graph Colorings¶
- 安排考试，使得没有学生同时要考两门
- 顶点表示科目，若有学生要考两门，则在表示考试科目的两个顶点之间有边，用不同颜色来表示考试的每个时间段，则问题转化为给图着色
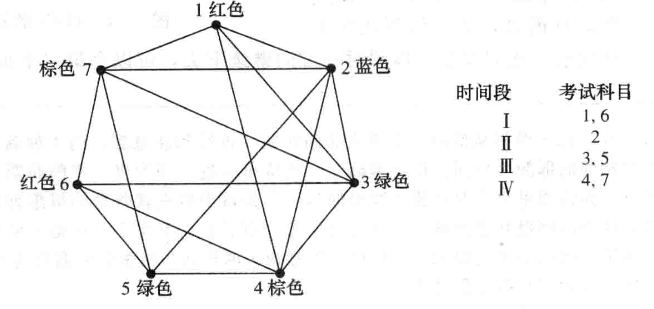
- 设置栖息地，使得没有动物冲突
- 顶点表示动物，若两种动物之间不能在同一个栖息地，则有一条边，不同颜色表示不同栖息地，则问题转化为给图着色
Supplementary Exercises 📑¶
A tournament is a simple directed graph such that if \(u\) and \(v\) are distinct vertices in the graph, exactly one of \((u, v)\) and \((v, u)\) is an edge of the graph. Assume all vertices are labeled, how many different tournaments with \(n\) vertices are there?
- \(2^{\frac{n(n-1)}{2}}\)，完全图 \(K_n\)，每条边有两个选择（\(u\to v\) or \(v \to u\)）
If \(G\) is a planar connected graph with 20 vertices, each of degree 3, how many regions \(G\) has?
- \(r=e-v+2=\frac{3\times 20}{2}-20+2=12\)
What is the length of the longest simple circuit in \(K_5\) ? 🔗
- \(K_5\) 有欧拉回路，因此最长的 simple circuit 是 10
- 一般地，\(n\) 为奇数时有欧拉回路，为 \(\frac{n(n-1)}{2}\)，\(n\) 为偶数时给每个点删去一条边 \(\frac{n(n-1)}{2}-\frac{n}{2}=\frac{n(n-2)}{2}\)
Determine whether these two graphs are isomorphic, and justify your answer.
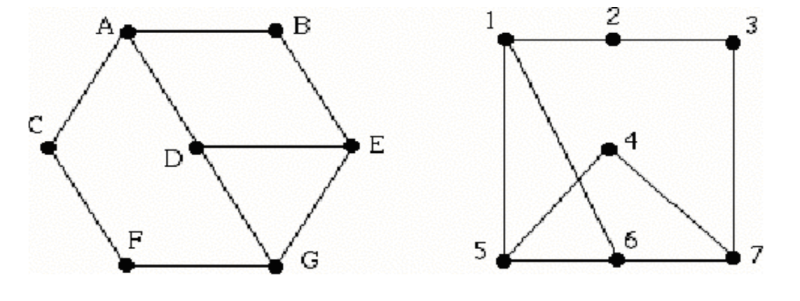
- 同构。\(A-7,B-4,C-3,D-6,E-5,F-2,G-1\)
The Math Department has 6 committees that meet once a month. How many different meeting times must be used to guarantee that no one is scheduled to be at meetings at the same time, if committees and their members are: \(C_1=\{Allen, Brooks, Marg\}\), \(C_2=\{Brooks, Jones, Morton\}\), \(C_3 =\{Allen, Marg, Morton\}\), \(C_4 =\{Jones, Marg, Morton\}\), \(C_5=\{Allen, Brooks\}\), \(C_6 =\{Brooks, Marg, Morton\}\).
- 图染色问题。点是 committee，如果有交集则有边，答案是 5
Use Dijkstra's Algorithm to find the shortest path length between the vertices \(a\) and \(z\) in this weighted graph.
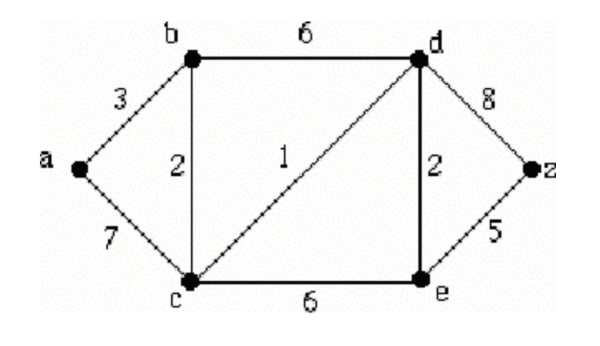
- 常规最短路，答案是 13
Determine the truth value of the statement: 'A bipartite graph with an odd number of vertices does not have a Hamilton circuit' and justify your answer.
- 真。想要在二分图中构造哈密顿回路，必须在从一个顶点集中的一个顶点开始，到达另一个顶点集中的一个顶点，然后再返回第一个顶点集中的另一个顶点，依此类推。而奇数个顶点的二分图中，两个顶点集的点数为一奇一偶，不相等，因此无法构造哈密顿回路