Ch9. Relations¶

约 2232 个字预计阅读时间 7 分钟

Binary Relation¶

Definition: A binary relation \(R\) from a set \(A\) to a set \(B\) is a subset of \(A \times B\)
- \(R \subseteq A\times B\)
- \(R=\{(a,b)\mid a\in A, b\in B, aRb\}\)

Relation on a Set¶

Definition: A relation on a set \(A\) is a relation from \(A\) to \(A\), a.k.a. a relation on a set A is a subset of \(A\times A\)
- \(R\subseteq A\times A\)
How many binary relations are there on a set \(A\) with \(n\) elements? - \(2^{n^2}\)

Representing Relations¶

2D TableConnection MatrixDirected graph/Digraph

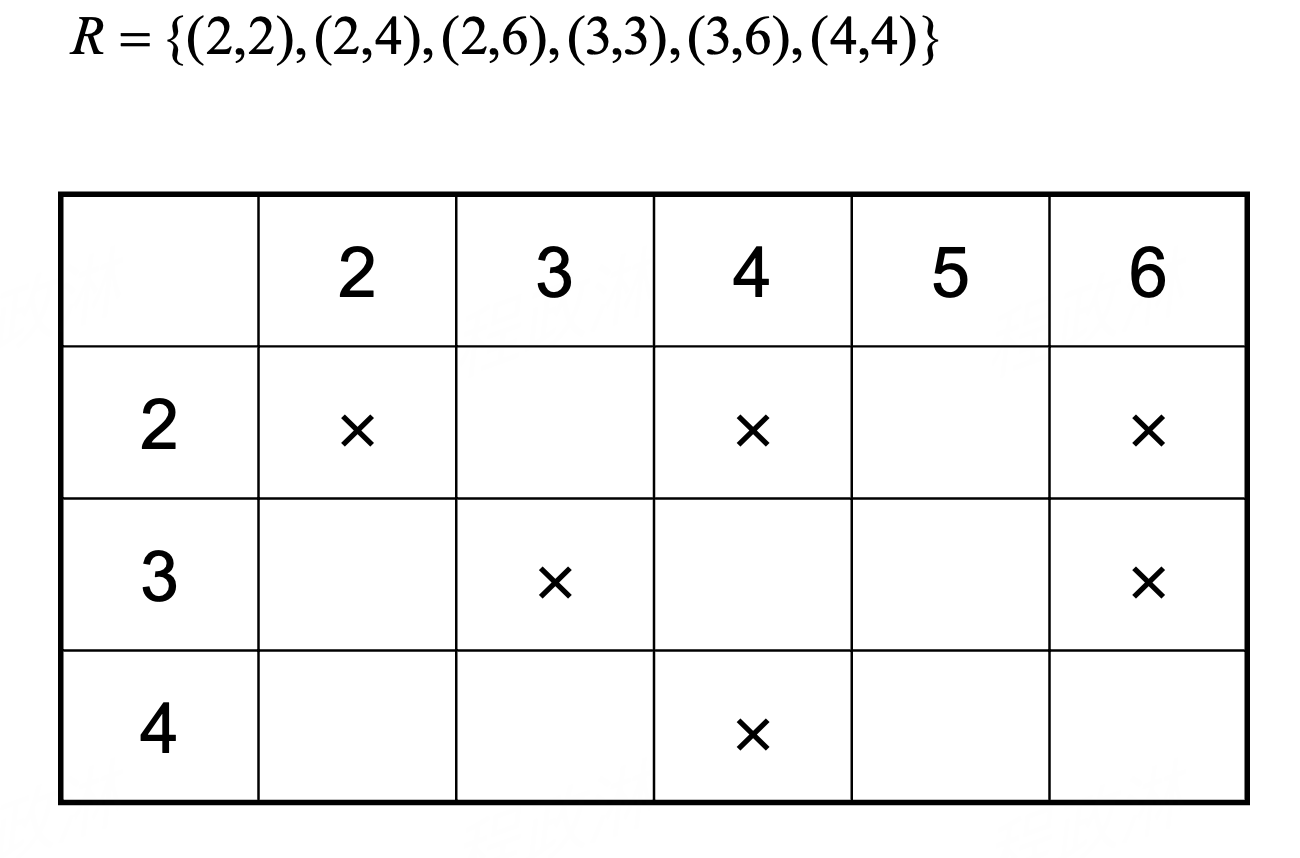
BKSA6k

0Ygsbj

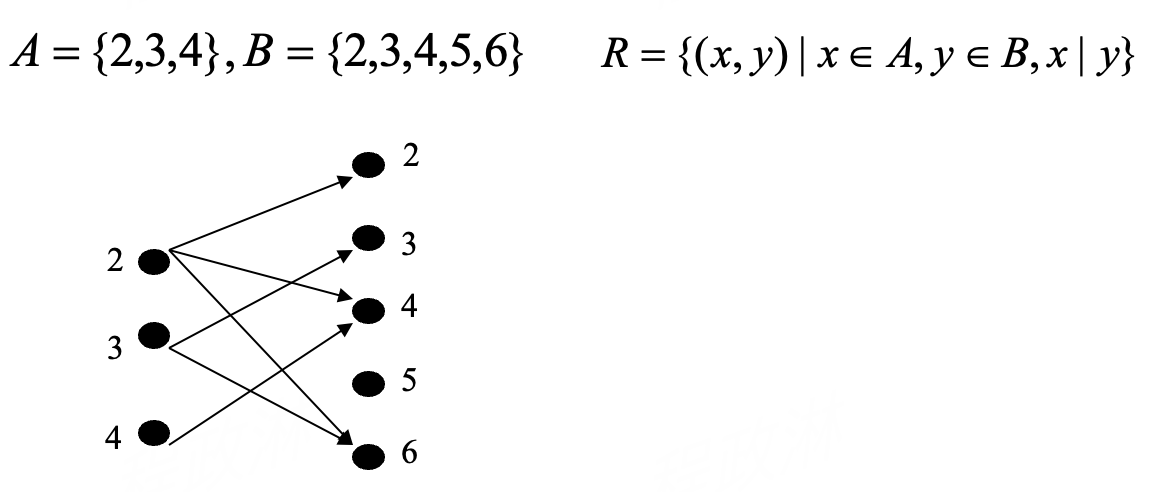
jHdnT2

Special Properties of Binary Relations¶

若无特殊说明，在说明性质时，均是 \(n\) 元集上的关系

Reflexive (自反) & Irreflexive (反自反)Symmetric (对称)Antisymmetric (反对称)Asymmetric (非对称)Transitive (传递)

Reflexive (自反)
- \((x,x)\in R\), for element \(x\in A\)
- \(\forall x(x\in A \to (x,x)\in A)\)
- 自反关系个数为：\(2^{n^2-n}\)

Irreflexive (反自反)
- \(\forall x(x\in A \to (x,x) \not \in A)\)
- 反自反关系个数：\(2^{n^2-n}\)
- 一个关系可以既不是 reflexive 也不是 irreflexive，有 \(2^{n^2}-2\cdot 2^{n^2-n}\)

\(R_1,R_2\) reflexive
- \(R_1 \cup R_2, R_1\cap R_2, R_1\circ R_2\) reflexive
- \(R_1 \oplus R_2,R_1-R_2\) irreflexive

\(\forall x\forall y((x,y)\in R \to (y,x) \in R)\)
对称关系个数为：\(2^n\cdot 2^{\frac{n^2-n}{2}}=2^{\frac{n(n+1)}{2}}\)
\(R^n\) 也是对称的
\(\bar R\) 也是对称的

\(\forall x\forall y((x,y)\in R \land (y,x) \in R \to x=y)\)
\(\forall x \forall y ((x,y)\in R \land x\neq y \to (y,x)\not \in R)\)
非对称关系个数为：\(2^n\cdot 3^{\frac{n^2-n}{2}}\)
- 有 3 个选择，是 (0, 0), (0, 1), (1, 0)

\(\forall x\forall y((x,y)\in R \to (y,x) \not\in R)\)
非对称关系个数为 \(3^{\frac{n^2-n}{2}}\)

\(\forall x\forall y \forall z((x,y)\in R\land (y,z)\in R\to (x,z)\in R)\)
\(\neg(m_{ij}\land m_{jk})\vee m_{ik}\)

Quoted from Wiki 🔗: No general formula that counts the number of transitive relations on a finite set is known

We can find formula for reflexive & symmetric & transitive (equivalence relations) relations, which is \(\sum_{k=0}^nS(n,k)\), \(S(n,k)\) 是第二类斯特林数
symmetric, transitive \(\not \Rightarrow\) reflexive!!!

Combining Relations¶

\(A\) 到 \(B\) 的关系是 \(A\times B\) 的子集，任意两个 \(A\) 到 \(B\) 的关系也可以用集合运算符连接
\(\cup, \cap,\oplus,-,\bar{}\)

Composition - \(S\circ R\)¶

\(R=\{ (a,b) \mid a \in A, b\in B,aRb \},\, S=\{ (b,c) \mid b \in B, c\in C,bSc \}\)
\(S\circ R = \{(a,c)\mid a\in A\land c\in C\land \exists b(b\in B\land aRb\land bSc\}\)
\(S\circ R\neq R\circ S\)
\(S \circ R = M_R\cdot M_S\)
如何计算？
- 按定义直接复合
- 关系矩阵做乘法
\(R^n\) is defined by: \(R^1=R\), \(R^{n+1}=R^n\circ R\)
[Theorem] The relation \(R\) on a set A is transitive iff \(R^n\subseteq R\), \(n=1,2,3,...\)

Proof

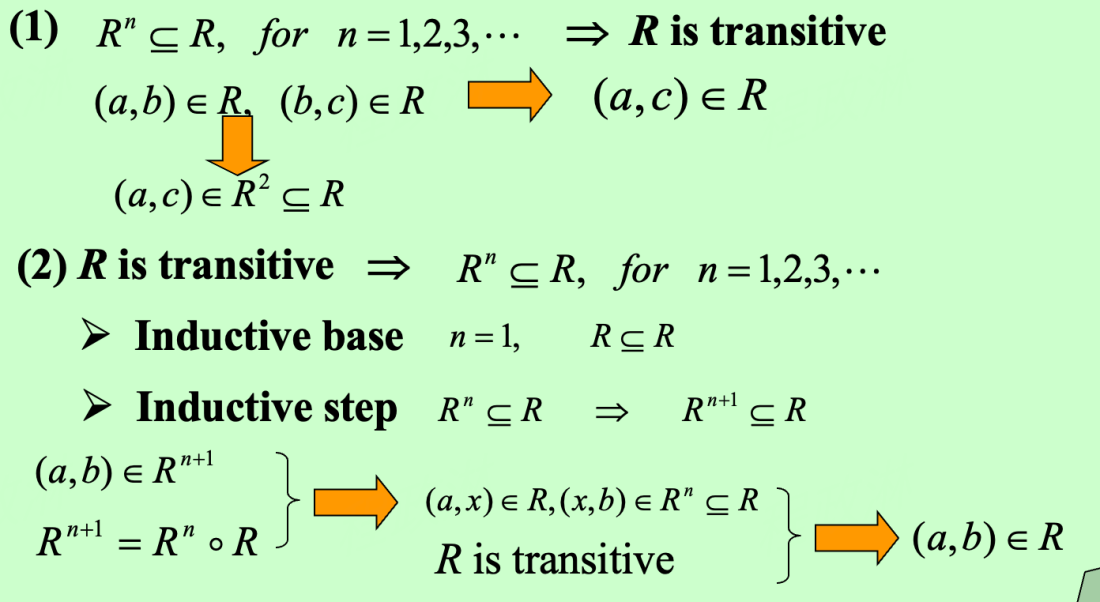
3GPI7g

Inverse - \(R^{-1}\)¶

\(R=\{ (a,b) \mid a \in A, b\in B,aRb \}\)
\(R^{-1}=R=\{ (b,a) \mid (a,b)\in R, a \in A, b\in B,aRb \}\)
如何计算？
- 由定义直接计算
- 关系矩阵转置

Properties¶

Suppose that \(R,S\) are the relations from \(A\) to \(B\)

\(T\) is the relation from \(B\) to \(C\)

\(P\) is the relation from \(C\) to \(D\)

\((R\cup S)^{-1}=R^{-1}\cup S^{-1}\)
\((\bar R)^{-1}=\bar{R^{-1}}\)
\((R-S)^{-1}=R^{-1}-S^{-1}\)
\((A \times B)^{-1}=B\times A\)
\(\bar R = A\times B -R\)
\((S\circ T)^{-1}=T^{-1}\circ S^{-1}\)
\((R\circ T)\circ P = R\circ (T\circ P)\)
\((R\cup S)\circ T=R\circ T\cup S\circ T\)

Closures of Relations (关系闭包)¶

定义：R 是集合 A 上的关系。R 可能具有或者不具有某些性质 P，例如自反性、对称性或传递性。如果存在包含R 的具有性质 P 的关系 S，并且 S 是所有包含 R 且具有性质 P 的关系的子集，那么 S 叫做 R 的关于性质 P 的闭包

Reflexive Closure (自反闭包)Symmetric Closure (对称闭包)Transitive Closure (传递闭包)

\(r(R)=R\cup I_A,\,I_A=\{(x,x)\mid x\in A\}\)
\(R=R\cup I_A \Leftrightarrow R\) is reflexive

\(s(R)=R\cup R^{-1}\)
\(R=R\cup R^{-1}\Leftrightarrow R\) is symmetric

定义有向图的 path: A sequence of edges \((x_0,x_1),(x_1,x_2),...,(x_{n-1},x_n)\), denoted by \(x_0,x_1,...,x_{n-1},x_n\)
- 传递关系可以和有向图中的路径相对应
circle/circuit: \(x_0=x_n\)
- \(\lvert A \rvert =n\), then any path of length\(\gt n\)must contain a cycle
[Theorem] 在 \(A\) 上的关系 \(R\)，存在 \(a\) 到 \(b\) 的长度为 \(n\) 的路径当且仅当 \((a,b)\in R^n\)
The Connectivity Relation: 对 \(R^*\) 的任意 \((a,b)\)，都存在一条从 \(a\) 到 \(b\) 的路径
- \(R^*= \bigcup_{n=1}^\infty R^n\)
\(t(R)=R^*\)
- \(\lvert A \rvert =n\), then \(t(R)=R^*=R\cup R^2\cup ... \cup R^n\)

How to Compute t(R)?¶

暴力求解Warshall's Algorithm (沃舍尔算法，求解 \(t(R)\))

时间复杂度为：\(O(n\cdot (n^3+n))=O(n^4)\)

🤔

Warshall 算法也即 Floyd-Warshall 🔗 算法，其中 Floyd 算法是求解多源最短路的算法，可以求出所有点之间的最短距离。Warshall 算法是 Floyd 的弱化版本，只关注最短路的存在性

interior vertices (内部点)：定义为一条路径除去起始和结尾的点，例如 \(a,b,c,d,e\) 的内部点是 \(b,c,d\)
Warshall's Algorithm 通过构造 \(W_0,W_1,...,W_n\)矩阵来求解 \(t(R)\)，其中 \(W_0=M_R,W_n=t(R)\)
\(W_k\) 的定义是：对于 \(W_k\) 中的每一个 \(w_{ij}^{(k)}\)，若存在一条从 \(v_i\) 到 \(v_j\) 的路径，且其内部点均在 \(\{v_1,v_2,...,v_k\}\) 中，那么 \(w_{ij}^{(k)}=1\)，否则为 0
\(W_k\) 可以由 \(W_{k-1}\) 计算，考虑两种情况：

没有用到 \(v_k\)用到了 \(v_k\)，\(v_k\) 为其中一点

Svizoi

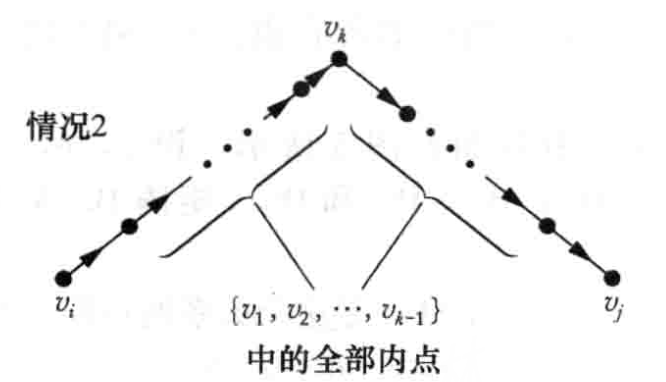
Hkoi6q

因此，从 \(W_{k-1}\) 计算 \(W_k\) 的方法是：\(w_{ij}^{(k)}=w_{ij}^{(k-1)}\vee(w_{ik}^{(k-1)}\land w_{kj}^{(k-1)})\)，时间复杂度为 \(O(n^3)\)
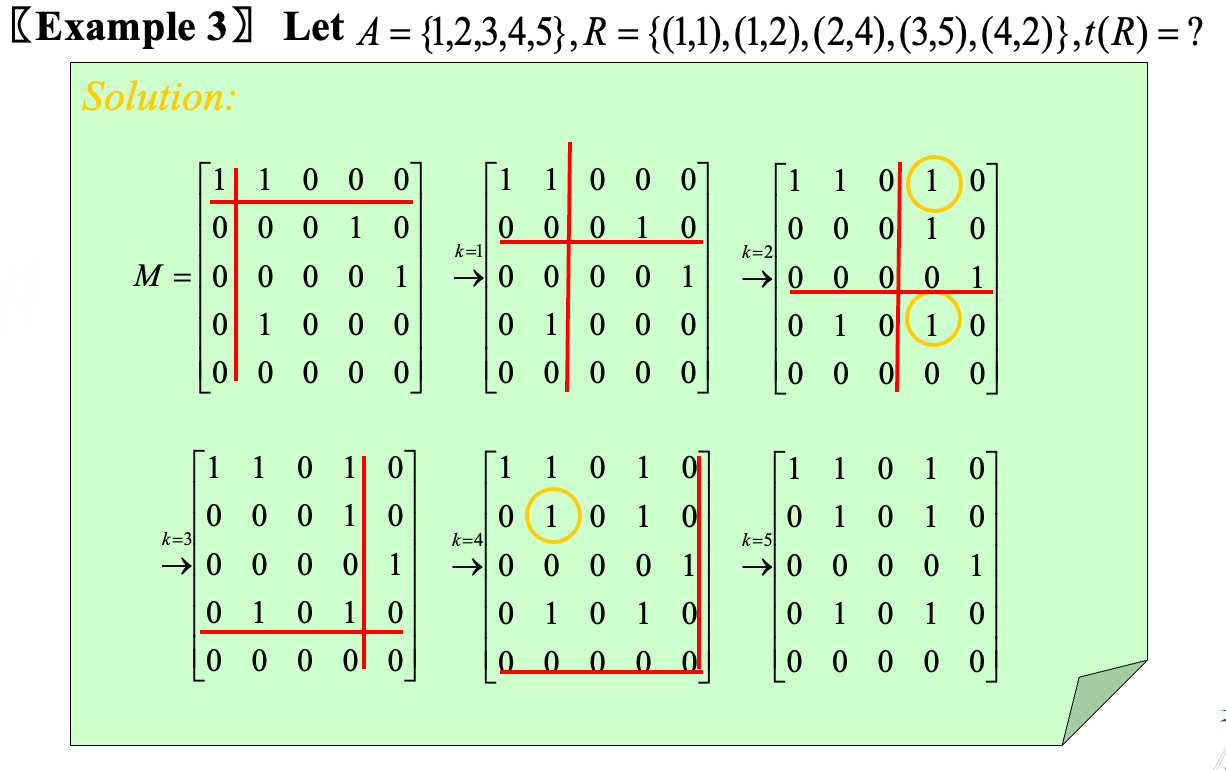
从关系矩阵上来看，计算方法表现为要么 \(w_{ij}^{(k-1)}\) 为 1，要么从对角线扫描行列，确定是否同时 1（如下图红线所示）

一个例子

Dw6gu0

Equivalence Relations¶

Definition: reflexive & symmetric & transitive
\(a \sim b\): \(a\) and \(b\) are equivalent
\(\left[ x \right]_R ,\, \left[ x \right]\): the equivalence class of \(x\)
Theorem \(R\) is an equivalence relation on a set \(A\), then \(aRb\Leftrightarrow \left[ a \right] = \left[ b \right] \Leftrightarrow \left[ a \right] \cap \left[ b \right] \neq \varnothing\)

Partitions¶

Partition (划分) 即将一个集合划分为两两互不相交的非空子集，其并集为原集
集合的划分和等价类一一对应
划分、等价类在关系图中的体现为不同的连通分量

等价关系计数¶

Bell 数：\(n\)元集合上等价类的个数 🔗：\(B_{n+1}=\sum_{k=0}^nC(n,k)B_k,\, B_0=1,B_1=1,B_2=2\)
手算类似帕斯卡三角形：
- 将 1 放在其第一个位置
- 每行三角形中最左边的值通过复制上一行中最右边的值。每行中的其余位置是左侧和左上方位置的两个值之和
```
1 - B1
1 2 - B2
2 3 5 - B3
5 7 10 15 - B4
15 20 27 37 52 - B5
52 67 87 114 151 203 - B6
```
\(n\) 元集合上分成 \(k\) 个等价类的个数：\(S(n,k)\)，第二类斯特林数
- \(S(n,k)=S(n-1,k-1)+k\cdot S(n-1,k),\,\,S(0,0)=1,\, S(k,0)=0\, (k>0)\)
- 手算先分组，再求组合数。例如 \(S(5,3)\)，分为 2 2 1, 3 1 1。然后分组求排列，和球盒模型中球不相同，盒子相同等价

Properties¶

\(R_1,R_2\) are equivalence relations on \(A\), then \(R_1\cap R_2\) is equivalence relation on \(A\)
\(R_1,R_2\) are equivalence relations on \(A\)
- then \(R_1\cup R_2\) is reflexive and symmetric, not transitive
- \((R_1\cup R_2)^*\) is equivalence relation on \(A\)
\(R_1\oplus R_2\) 永远都不是等价关系，因为不 reflexive

Partial Orderings¶

Definition: reflexive & antisymmetric & transitive
\((S,R)\): set of partial order \(R\) on set \(S\), called partially ordered set or poset
\(a\preceq b\):\((S,R)\)is a poset, \((a,b)\in R\)
Comparable: \(a,b\) of \((S,\preceq)\), \(a\preceq b\)or\(b \preceq a\)
Incomparable: \(a,b\) of \((S,\preceq)\), neither \(a\preceq b\) nor \(b \preceq a\)
任意两个元素之间 Comparable 时：\(S\)is called totally ordered or linearly ordered set, \(R\) is called linear order (线序) or total order (全序), \((S,R)\) is called chain (链)
- 有 \(n!\) 种
\(n\) 元集合上的偏序计数
- OEIS A001035 🔗
- 1, 3, 19, 219

Lexicographic Order (字典序)¶

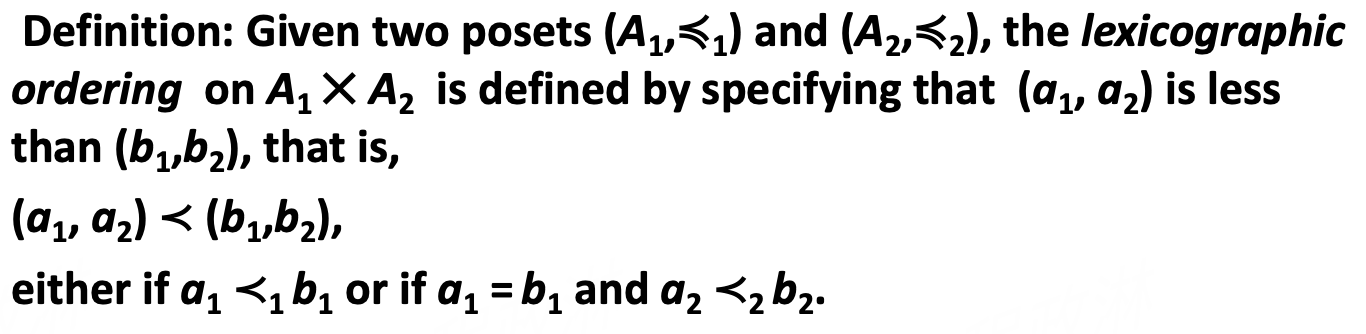
pqS637

Hasse Diagram (哈斯图)¶

Example

\(A=\{1,2,3,4,5,6,7,8,9\}\), \(R=\{(a,b)\mid a | b,a,b \in A\}\)

用有向图表示出所有的关系

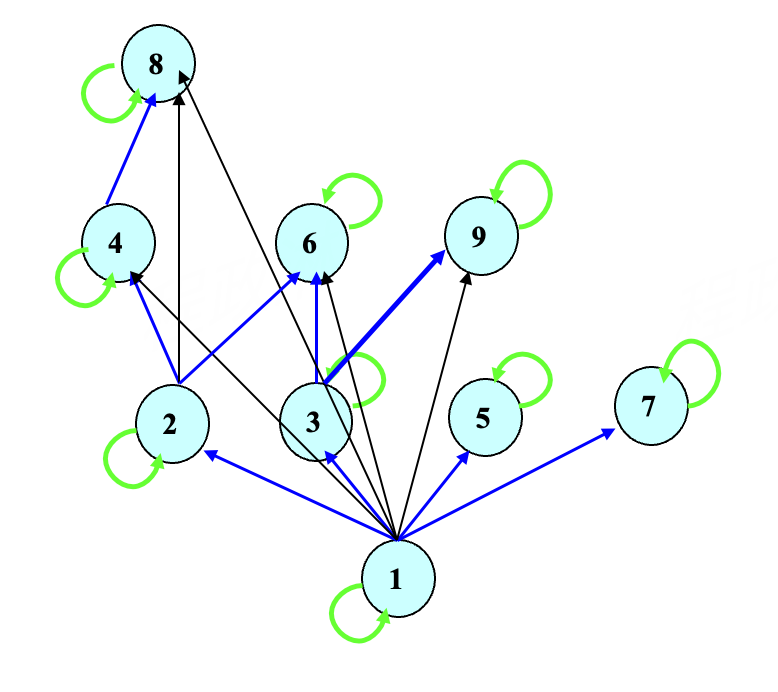
sYkJwE

删除自环

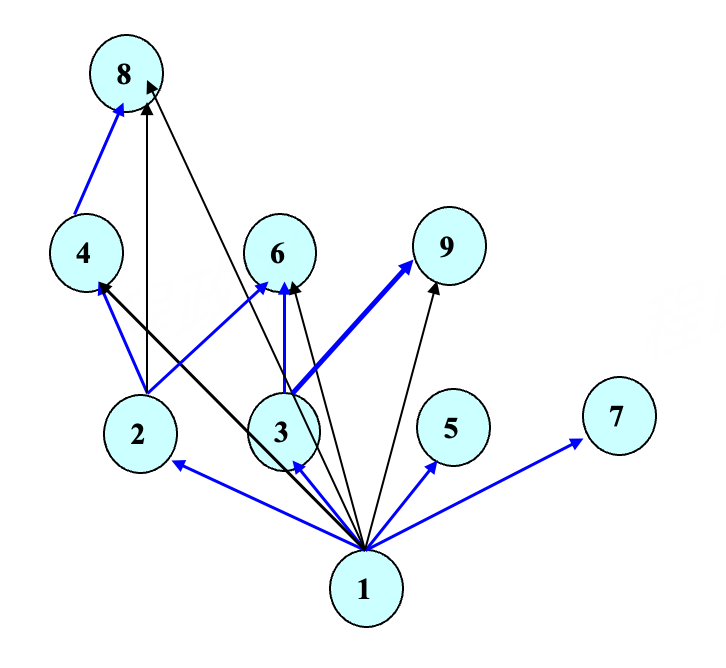
TfvSdD

删除可以通过传递性得到的边

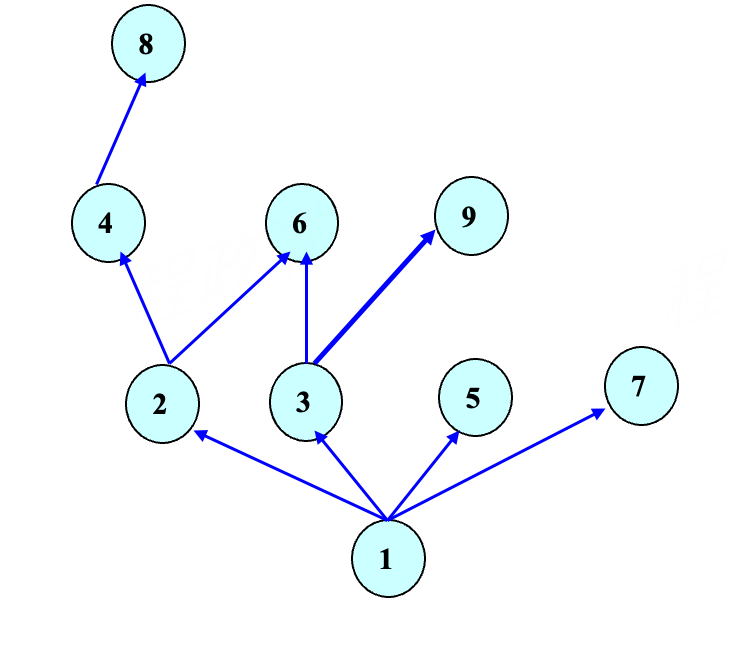
SJ9FZn

转为无向图

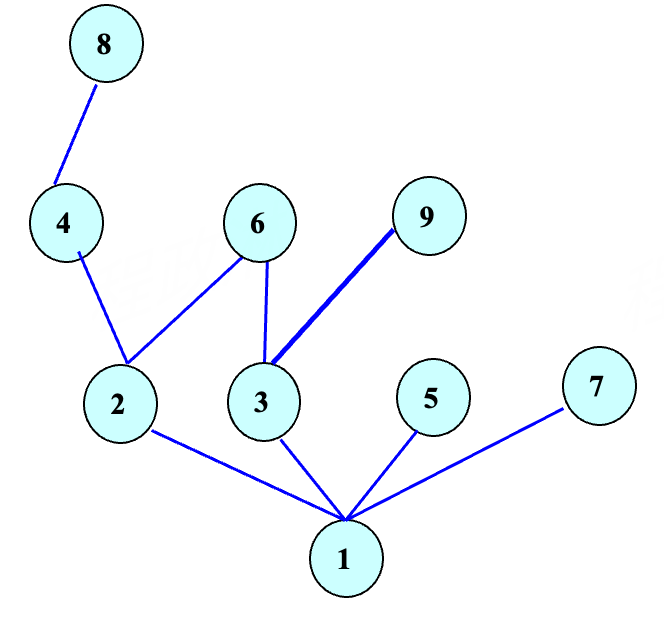
kwdSOx

chain and antichain¶

totally ordered set \(\Leftrightarrow\) chain (任意两个元素可以比较)
antichain (任意两个不同元素都不可比较)

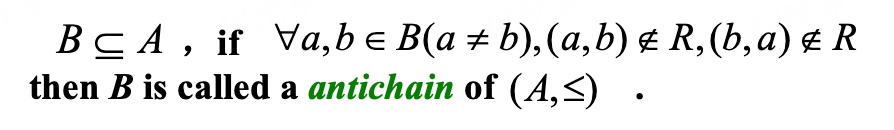
ZMZg22

例如 30 的因数整除关系，\(\{1,2,6,30\}\) 是一个 chain，\(\{ 2,3,5 \}\) 是 antichain

Maximal and Minimal Elements (极大值、极小值)¶

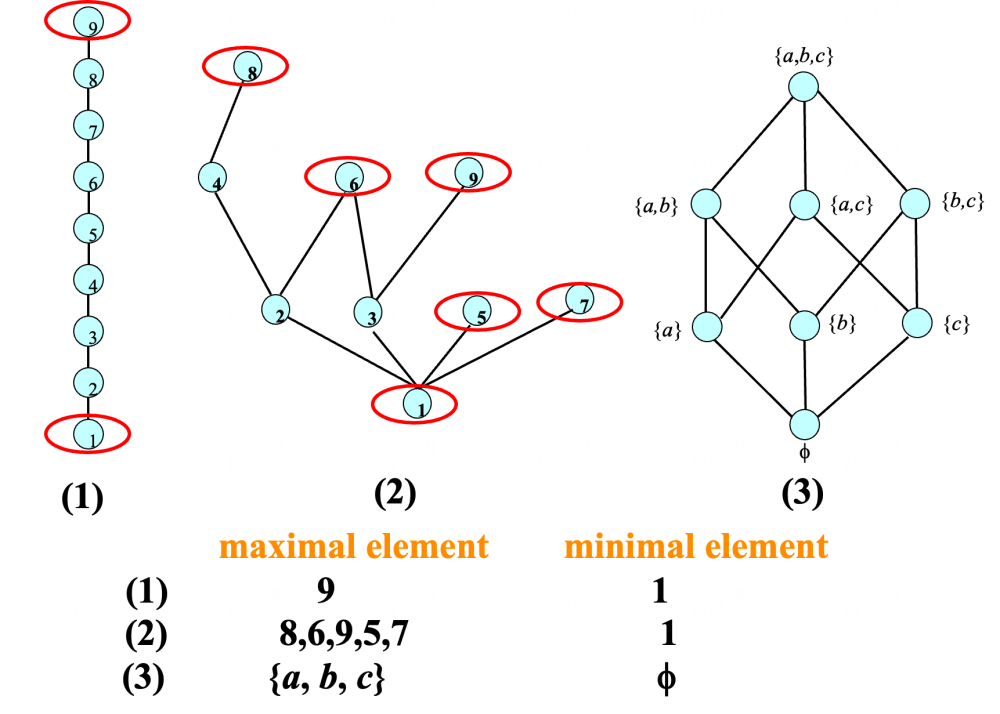
diObV8 VN41kC

Greatest and Least Element (最大值、最小值)¶

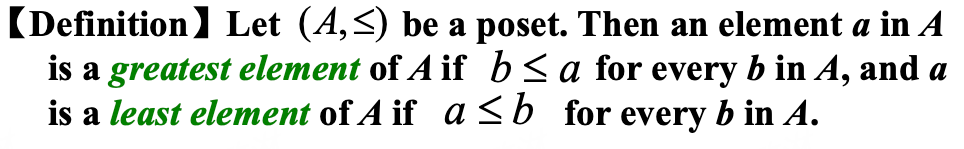
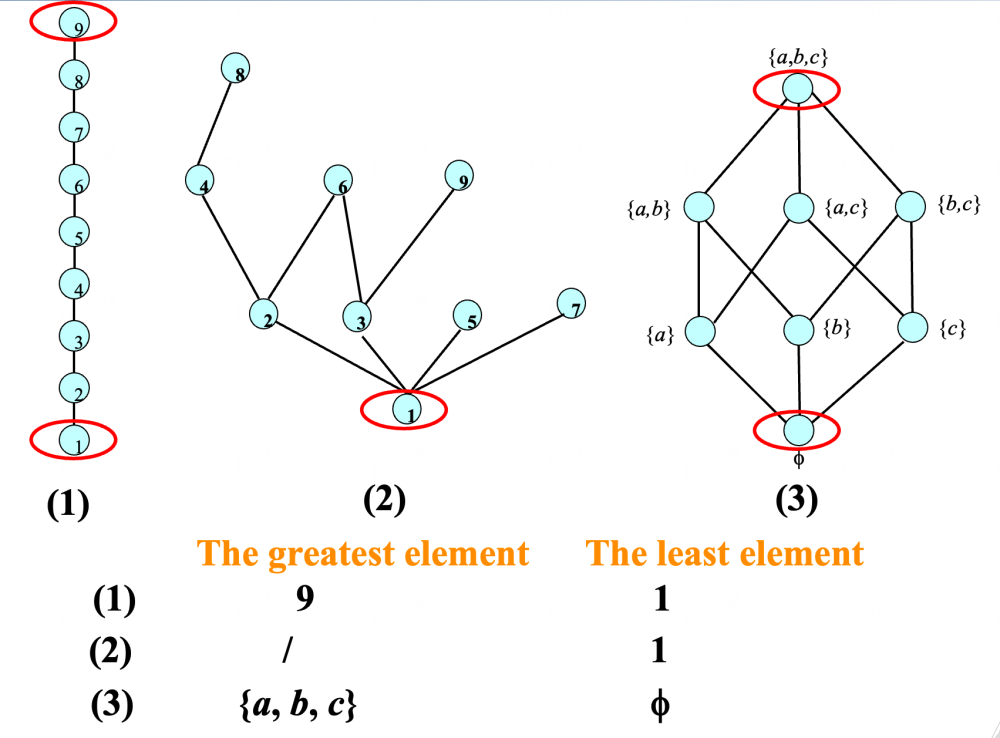
dBsCxm h96A4u

最大值、最小值如果存在，那么是唯一的

Upper and Lower Bounds (上、下界)¶

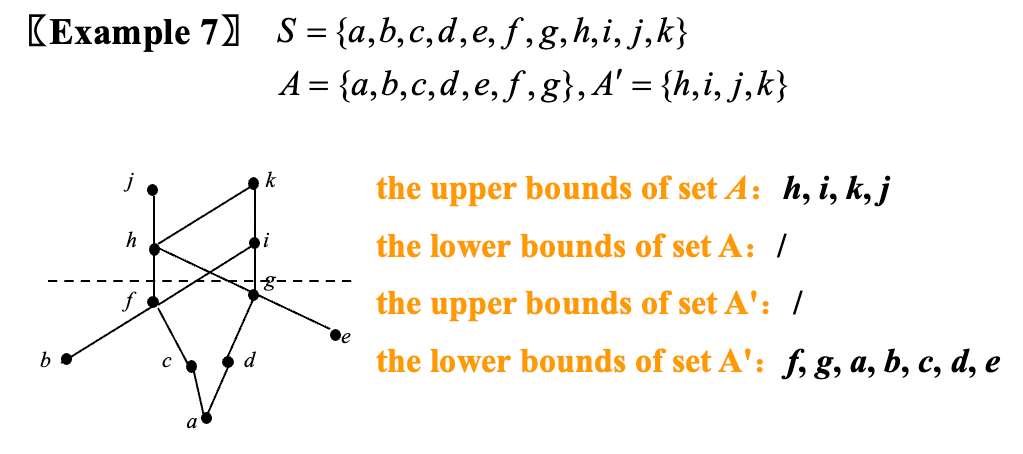
CXw1Jo VLVfwC

Least Upper and Greatest Lower Bounds (最小上界、最大下界)¶

CcNXna FTzo3h

Well-ordered Sets (良序集)¶

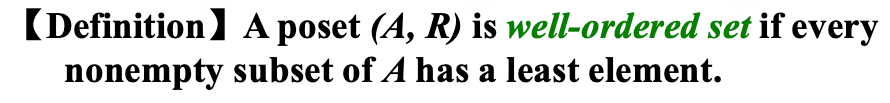
jFAwlW

well-ordered \(\Rightarrow\) totally ordered (良序推全序)

Lattices (格)¶

每对元素都有 最小上界 和 最大下界 称为「格」
totally ordered \(\Rightarrow\) 格
\((\mathbb{Z},\ge )\)
\((\mathbb{Z^+},\mid)\) (glb 为 \(\gcd\)，lub 为 \(\operatorname{lcm}\))
\((\mathcal{P}(s),\subseteq)\) (\(A,B\subseteq S\), glb 为 \(A\cap B\), lub 为 \(A\cup B\))
\((\mathcal{P}(s),\supseteq)\) (\(A,B\subseteq S\), glb 为 \(A\cup B\), lub 为 \(A\cap B\))
\((S, R)\) 为格，则 \((S,R^{-1})\) 也是格

Topological Sorting¶

从一个偏序构造一个全序
每次找一个极小元素，然后删除该元素和与其相关联的关系后，继续寻找极小元素，直到形成全序

Ch9. Relations¶

Binary Relation¶

Relation on a Set¶

Representing Relations¶

Special Properties of Binary Relations¶

Combining Relations¶

Composition - \(S\circ R\)¶

Inverse - \(R^{-1}\)¶

Properties¶

Closures of Relations (关系闭包)¶

How to Compute t(R)?¶

Equivalence Relations¶

Partitions¶

等价关系计数¶

Properties¶

Partial Orderings¶

Lexicographic Order (字典序)¶

Hasse Diagram (哈斯图)¶

chain and antichain¶

Maximal and Minimal Elements (极大值、极小值)¶

Greatest and Least Element (最大值、最小值)¶

Upper and Lower Bounds (上、下界)¶

Least Upper and Greatest Lower Bounds (最小上界、最大下界)¶

Well-ordered Sets (良序集)¶

Lattices (格)¶

Topological Sorting¶

评论